ABSTRAK
Makalah ini menjelaskan penerapan tomografi resistivitas listrik (ERT) tiga dimensi di lingkungan perkotaan untuk mendeteksi fondasi dinding atau struktur serupa. Dalam studi ini, strategi pengukuran khusus berdasarkan array pengukuran 3D yang dioptimalkan dengan elektroda permukaan diusulkan dan diuji. Karena jenis survei ini dapat digunakan untuk prospeksi arkeologi, desain khusus dipilih untuk membuat survei senon-invasif mungkin. Oleh karena itu, skema pengukuran ERT 3D menggunakan tata letak yang menempatkan garis elektroda di setiap sisi dinding. Dengan menggunakan metode optimasi berdasarkan matriks Jacobian, hanya pengukuran garis silang dan garis optimal yang dipilih. Skema yang diusulkan diuji menggunakan model sintetis dan juga diterapkan pada penyelidikan fondasi di dua lokasi tembok Bizantium Thessaloniki, Yunani Utara, dekat Gerbang Kassandria. ERT 2D tambahan dilakukan pada setiap segmen dinding yang memotong dinding secara tegak lurus untuk menguji hasil ERT 3D.
Hasil data sintetis yang disajikan mendukung keefektifan skema pengukuran dan sekaligus memberikan informasi penting tentang kedalaman investigasi maksimum dan tentang pengaruh bentuk struktur, yang harus dipertimbangkan sebagai informasi apriori dalam proses inversi. Bagian terpilih dari inversi 3D data lapangan dapat dibandingkan dengan hasil ERT 2D masing-masing. Secara keseluruhan, skema pengukuran ERT 3D yang diusulkan telah terbukti menjadi metode prospeksi non-destruktif yang efektif.
1 Pendahuluan
Metode geolistrik biasanya digunakan untuk mendeteksi struktur bangunan karena kontras resistivitas listrik dari bahan bangunan dan lingkungannya (Clark 1990 ; Milsom 2003 ). Di antara metode geolistrik, penerapan teknik tomografi resistivitas listrik (ERT) dua dan tiga dimensi tersebar luas untuk menggambarkan fondasi struktur, karena mereka memberikan informasi berharga mengenai kedalaman dan luas lateral serta penilaian stabilitas umum (Chambers et al. 2002 ; Santarato et al. 2011 ; Argote-Espino et al. 2013 ; Wang dan Hu 2015 ; Almeida et al. 2019 ; García-Nieto et al. 2024 ). Lebih jauh lagi, ERT 2D dan 3D pada monumen yang berdiri telah digunakan secara luas karena memberikan hasil resolusi tinggi, berguna untuk preservasi monumen serta mampu menggambarkan bagian-bagian yang tak terlihat secara akurat, dengan dampak yang rendah pada struktur (Tsourlos dan Tsokas , 2011 ; Tsokas et al., 2013 ; Vargemezis et al., 2013 ; Tsokas et al., 2015 ; Angelis et al., 2017 ).
Konfigurasi umum untuk melakukan survei ERT 3D adalah dengan menggunakan array kutub-kutub penuh menggunakan semua elektroda permukaan yang diletakkan pada grid 3D (Park dan Van 1991 ; Li dan Oldenburg 1992 ; Loke dan Barker 1996 ; Almeida et al. 2019 ). Konfigurasi lain seperti array L dan sudut (Chávez et al. 2014 ), dipol ekuatorial atau dipol-dipol konvensional, Wenner-Schlumberger dan array multi-gradien dengan offset lateral yang berbeda telah diusulkan (Chambers et al. 2006 ; Johnson et al. 2010 ; Loke et al. 2014 ). Konfigurasi ini menawarkan lebih banyak kemungkinan kombinasi elektroda sekaligus menyediakan metode untuk melewati rintangan dan tetap mempertahankan resolusi yang memadai. Sementara skema pengukuran ERT 3D penuh beresolusi tinggi memberikan hasil yang lebih unggul, peralatan yang digunakan untuk survei tersebut memerlukan meter resistivitas otomatis, yang dapat mendukung sejumlah besar elektroda melalui kotak sakelar dan kabel multiinti terkait. Sebagai alternatif, survei ERT 3D dapat dilakukan dengan menggabungkan sejumlah garis ERT 2D paralel yang memadai. Metode grid padat yang terdiri dari ERT 2D paralel dengan inversi data 3D simultan ini dapat menghasilkan model 3D akurat dengan menggunakan peralatan yang tersedia secara luas (Dahlin dan Bernstone 1997 ; Chambers et al. 1999 ; Yi et al. 2001 ; Chambers et al. 2002 ; Dahlin, Bernstone, dan Loke 2002 ; Gharibi dan Bentley 2005 ; Günther, Rücker, dan Spitzer 2006 ; Papadopoulos et al. 2006 ; Rücker, Levitt, dan Greenwood 2009 ).
Menggambarkan fondasi dinding atau fondasi struktur serupa, yang merupakan subjek utama studi ini, bisa jadi cukup menantang, khususnya ketika melakukan survei geofisika pada monumen berdiri yang terawat baik. Melakukan ERT 2D yang tegak lurus terhadap jurus dinding bisa efektif hanya selama ketinggian dinding dibatasi: dalam semua kasus lain, secara praktis mustahil untuk membuat garis ERT 2D yang melintasi dinding. Sementara survei semacam itu layak dilakukan dengan kabel ekstensi, dimensi substansial struktur baik tinggi maupun lebar, menyebabkan tidak adanya elektroda yang berarti resolusi berkurang dan peningkatan risiko kehilangan target potensial. Untuk mengatasi tantangan ini dalam beberapa kasus yang dilaporkan, lubang bor di kedua sisi dinding dibor (Tsokas et al. 2011 ; Leontarakis dan Apostolopoulos 2013 ) yang memungkinkan mode pengukuran ERT lintas lubang. Metode lain telah diusulkan untuk meningkatkan resolusi di area tanpa elektroda, hanya memanfaatkan elektroda permukaan dan teknik roll along saat mengukur dalam mode garis silang (Jackson, Earl, dan Reece 2001 , Ogilvy et al. 2002 ; Loke et al. 2014 , Tejero-Andrade et al. 2015 , Maurits et al., 2017 ).
Dalam karya ini, kami mengusulkan strategi pengukuran ERT 3D untuk menggambarkan fondasi dinding yang bergantung secara eksklusif pada pengukuran permukaan dengan elektroda yang disusun pada kisi-kisi reguler. Resolusi yang ditingkatkan di area yang diinginkan diperoleh dengan menggunakan protokol susunan elektroda yang dioptimalkan, yang terdiri dari susunan pengukuran sewenang-wenang sebaris dan lintas-garis yang berfokus terutama pada area target. Lebih jauh, integritas strategi pengukuran diperiksa secara ekstensif dengan model sintetis yang realistis dan diterapkan pada dinding utama Bizantium Thessaloniki dan bangunan luarnya, di bagian Gerbang Kassandrian.
2 Optimasi Susunan Elektroda
Prosedur optimasi elektroda harus diperkenalkan dalam pekerjaan ini karena tata letak elektroda yang digunakan rumit dan oleh karena itu, tidak ada skema pengukuran standar, berdasarkan konfigurasi susunan konvensional, yang dapat digunakan. Di antara semua kemungkinan kombinasi elektroda, metode optimasi digunakan untuk memilih hanya konfigurasi empat elektroda yang optimal, meminimalkan jumlah pengukuran sambil mempertahankan resolusi model yang memuaskan di wilayah bawah permukaan yang ditargetkan.
Jumlah kombinasi elektroda dalam protokol komprehensif tidak dapat dilakukan di lapangan karena ini akan sangat memakan waktu, bahkan dengan instrumen multisaluran modern. Untuk survei elektroda n = 48, pengukuran non-timbal balik dapat dihitung sebagai n × (n − 1) × (n − 2) × (n − 3) / 8 , yang menghasilkan jumlah pengukuran yang sangat besar dan tidak praktis untuk survei lapangan. Pembatasan lain dalam menggunakan protokol komprehensif adalah bahwa larik tertentu dapat menghasilkan artefak selama proses inversi karena rasio sinyal terhadap derau yang rendah atau sangat rentan terhadap perubahan kecil pada posisi elektroda. Melalui proses pra-optimalisasi di mana larik pengukuran ditolak sehubungan dengan faktor geometris yang besar (Stummer, Maurer, dan Green 2004 ; Loke, Wilkinson, dan Chambers 2010 ), protokol komprehensif difilter dan jumlah larik pengukuran dikurangi. Pengurangan lebih lanjut dicapai ketika ambang sensitivitas faktor geometrik ditetapkan untuk setiap larik, dengan memperhitungkan kemungkinan kesalahan pada posisi elektroda (Wilkinson et al. 2008 ; Loke et al. 2014 ). Protokol yang difilter yang berasal dari kumpulan data komprehensif masih dapat mempertahankan sejumlah besar pengukuran, namun tidak dapat diterapkan untuk penggunaan lapangan. Oleh karena itu, perlu untuk mengurangi lebih lanjut jumlah pengukuran, dengan fokus pada pemilihan larik terbaik untuk survei tertentu.
Banyak metode optimasi telah diusulkan, mulai dari penolakan acak array hingga pendekatan yang lebih kuantitatif yang bergantung pada matriks Jacobian (Furman, Ferré, dan Heath 2007 ; Athanasiou et al. 2009 ), matriks Resolusi (Stummer, Maurer, dan Green 2004 ; Wilkinson et al. 2006 ; Wilkinson et al. 2012 ) atau mengikuti desain Bayesian (Qiang et al. 2022 ). Dalam karya ini, metode optimasi diimplementasikan hanya berdasarkan matriks Jacobian. Matriks Jacobian adalah salah satu kalkulasi yang paling memakan waktu selama proses inversi, terutama dalam survei resistivitas 3D, yang membuat desain survei ERT 3D yang optimal menjadi proses yang membosankan. Masalah lainnya adalah banyaknya parameter dalam ruang 3D yang tidak dapat diselesaikan dengan kombinasi array tata letak elektroda apa pun, terutama pada batas-batas grid. Oleh karena itu, metode optimasi matriks Jacobian yang dimodifikasi digunakan, dengan menolak parameter bukan hanya untuk menghemat waktu (Papadopoulos et al. 2011 ), tetapi juga untuk menargetkan survei ke wilayah minat tertentu (Gambar 1 ) dan meningkatkan resolusi di area tersebut (Furman, Ferré, dan Heath 2007 ).
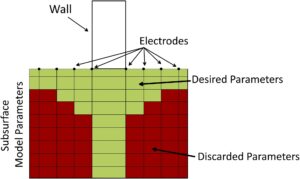
Proses optimasi dimulai dengan menetapkan pengukuran untuk parameter yang diinginkan dari area investigasi. Parameter tersebut diperingkat dan dikategorikan ke dalam klaster berdasarkan norma sensitivitas L1 yang diperoleh dari matriks Jacobian. Parameter yang tidak terselesaikan dengan baik membutuhkan lebih dari satu pengukuran, bukan parameter yang terselesaikan dengan baik, yang dapat memiliki satu pengukuran. Interval dan batasan yang menentukan parameter yang terselesaikan dengan baik atau buruk dapat diterapkan berdasarkan sensitivitas kumulatif. Klaster parameter dapat berupa satu atau lebih, tergantung pada parameterisasi dan jumlah pengukuran yang diinginkan. Prosesnya bersifat iteratif, sehingga dalam setiap iterasi, sejumlah besar pengukuran ditambahkan ke protokol yang dioptimalkan. Sensitivitas kumulatif untuk setiap parameter di setiap klaster meningkat dengan penambahan lebih banyak pengukuran, tetapi parameter tertentu tidak dapat diselesaikan dengan penambahan pengukuran apa pun. Parameter ini dibuang selama proses optimasi, dan penambahan pengukuran yang hanya memengaruhi area di bawah dinding menciptakan protokol yang solid untuk jenis investigasi ini sekaligus mengurangi waktu komputasi.
3 Skema Pengukuran ERT 3D
Diketahui bahwa setiap pengukuran memengaruhi parameter yang berbeda dengan dampak yang lebih besar atau lebih kecil pada sensitivitas vertikal atau lateral. Misalnya, pengukuran sebaris pada garis elektroda luar seperti yang terlihat pada Gambar 2 tidak dapat memengaruhi parameter di bagian tengah kisi (dinding), atau sensitivitas pada parameter ini akan diabaikan. Namun, pengukuran dalam mode garis silang dapat meningkatkan sensitivitas pada parameter pusat ini.
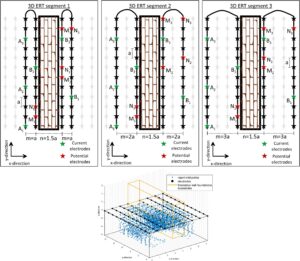
Strategi pengukuran yang kami perkenalkan mencakup kombinasi elektroda permukaan garis silang optimum yang dapat menyelesaikan parameter model dari wilayah yang diminati. Meskipun jumlah total elektroda yang digunakan dapat menjadi tantangan karena keterbatasan instrumen, metode ini dapat dilakukan dengan cara tersegmentasi, yang terdiri dari beberapa segmen 3D garis silang (Gambar 2 ). Di setiap segmen, terdapat simetri antara garis elektroda aktif dengan dinding sebagai bidang simetri. Dua garis elektroda yang paling dekat dengan dinding tetap diam selama semua segmen, sementara jarak antara elektroda terluar meningkat. Misalkan a adalah jarak elektroda di setiap garis. Pemisahan garis elektroda juga a , sementara dua baris elektroda stasioner sentral memiliki pemisahan yang lebih besar yaitu 1,5 a . Dapat dilihat bahwa elektroda bagian dalam hampir bersentuhan langsung dengan dinding. Pengukuran dalam mode garis silang di Segmen 1 menyelesaikan parameter yang memengaruhi wilayah dangkal di bawah dinding. Dengan meningkatkan pemisahan garis elektroda luar seperti di Segmen 2 atau 3 dan menggabungkan pengukuran dari beberapa segmen, kedalaman investigasi yang lebih besar tercapai. Secara praktis, resolusi pada kedalaman yang lebih besar dicapai dengan meningkatkan pemisahan antara garis elektroda dan pengukuran dengan susunan sembarangan non-konvensional yang titik datumnya sesuai dengan area di bawah target (Gambar 2 ).
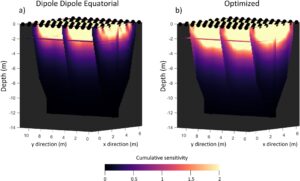
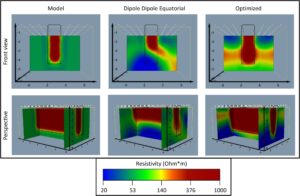
Meskipun fakta bahwa array konvensional seperti dipole equatorial telah diusulkan dan dapat digunakan di lapangan untuk ERT 3D penuh, ruang terbatas untuk tata letak elektroda serta kombinasi elektroda terbatas dari array ini, mengorbankan kedalaman investigasi maksimum. Perbandingan distribusi sensitivitas kumulatif 3D (Furman, Ferré, dan Warrick 2004 ) antara dipole equatorial dan protokol yang dioptimalkan dengan 96 elektroda, keduanya diukur dengan tiga kombinasi segmen kabel disajikan dalam Gambar 3. Protokol array konvensional karena keterbatasan dalam geometri tata letak elektroda memberikan sensitivitas kumulatif terbatas di area pusat dibandingkan dengan protokol yang dioptimalkan. Secara khusus, protokol yang dioptimalkan menunjukkan sensitivitas kumulatif yang unggul (Gambar 3a ) karena kedalaman meningkat jika dibandingkan dengan protokol konvensional (Gambar 3a ), kedalaman investigasi yang dicapai dengan array konvensional lebih rendah daripada protokol yang dioptimalkan.
Selain analisis sensitivitas dari array konvensional dan optimum, model sintetis menunjukkan keunggulan protokol yang dioptimalkan dibandingkan dengan yang konvensional dengan array ekuator dipol (Gambar 4 ). Model tersebut terdiri dari blok resistif persegi panjang terkubur sebesar 5000 Ohm*m, memanjang hingga kedalaman 4,5 m di antara delapan baris elektroda dalam halfspace homogen sebesar 30 Ohm*m. Hasil yang diperoleh dengan array ekuator dipol konvensional menunjukkan bahwa blok persegi panjang tidak dapat digambarkan secara tepat dan kedalaman total diremehkan sekitar 3 m. Sebaliknya, hasil inversi dari model yang sama, tetapi menggunakan protokol yang dioptimalkan, merekonstruksi model awal secara akurat dalam hal kedalaman, dengan beberapa artefak lateral.
Karena alasan ini, semua model sintetis dan pengukuran lapangan dibuat mengikuti strategi pengoptimalan yang dijelaskan di atas. Secara umum diakui bahwa, untuk memperoleh resolusi yang lebih baik dari parameter yang lebih dalam, pemisahan elektroda, atau pemisahan garis dalam skema kami, perlu ditingkatkan dan menetapkan susunan pengukuran yang memengaruhi parameter dengan kedalaman yang lebih besar. Analisis sensitivitas dari empat protokol individual dengan pemisahan garis elektroda yang berbeda mendukung peningkatan ini terkait kedalaman investigasi maksimum (Gambar 5a,b,c ).

Dapat dilihat bahwa sementara pemisahan garis elektroda ini ditingkatkan secara bertahap dari m = 2 a ke m = 4 a atau m = 6 a, kedalaman investigasi maksimum juga meningkat. Namun, peningkatan bertahap ini memiliki batas (Aizebeokhai et al. 2011 ) dan harus dipertimbangkan, sebelum susunan pengukuran garis silang mulai bertindak secara independen dan berhenti memberikan resolusi di area minat utama (Gambar 5d ).
4 Model Sintetis
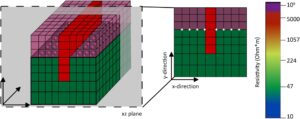
Integritas protokol yang dioptimalkan dan dengan demikian metode dan skema pengukuran diuji menggunakan model sintetis yang dapat mereplikasi kondisi sebenarnya dari motif pekerjaan ini. Semua model sintetis menggunakan prisma persegi panjang yang meniru dinding di tengah grid, dengan resistivitas 5000 Ohm*m yang memanjang di antara elektroda dalam ruang setengah homogen 30 Ohm*m. Untuk mereproduksi model secara akurat, kami membatasi parameter sedemikian rupa sehingga blok yang mewakili dinding secara teoritis menonjol dari permukaan datar, sementara resistivitas udara (109 Ohm *m) juga dibatasi dalam parameter model. Elektroda yang ditugaskan secara hipotetis dikubur dan parameter di atasnya mensimulasikan udara dan yang di bawahnya mewakili ruang setengah homogen (Gambar 6 ). Metode ini diterapkan karena adanya topografi ekstrem (yaitu, permukaan datar dengan dinding yang memanjang tegak lurus ke permukaan ini hingga ketinggian 5–10 m). Kami mengadopsi pendekatan ini karena elemen heksahedral yang ditetapkan dalam penyelesai maju cenderung meregang berlebihan saat informasi topografi ditambahkan, sehingga sulit untuk memodelkan permukaan secara akurat. Pendekatan lain adalah parameterisasi dengan elemen tetrahedral, yang dapat mereproduksi permukaan secara tepat, bahkan dengan geometri yang menantang.
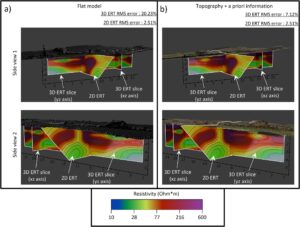
Gambar 7 menunjukkan hasil inversi untuk model sintetis dengan resistivitas 5000 Ohm*m, yang meluas hingga kedalaman 3 m dan tinggi 10 m, mengikuti prosedur kendala yang dijelaskan di atas. Untuk tujuan visualisasi, parameter model yang telah dibatasi agar sesuai dengan resistivitas udara di atas elektroda telah ditutup. Hasil menunjukkan pengaruh yang kuat di area target utama, baik di atas maupun di bawah elektroda. Menggabungkan hanya topografi yang tepat menghasilkan hasil yang memuaskan, dengan penyimpangan kecil dari model awal, membatasi kedalaman target hingga sekitar 2,5 m dan memperluas anomali yang kurang resistif ke bagian bawah model (Gambar 7b ). Di sisi lain, hasil tanpa topografi apa pun, yang berarti geometri dinding tidak digabungkan selama parameterisasi untuk prosedur inversi, menghasilkan model yang membatasi kedalaman target lebih dangkal, pada < 2 m (Gambar 7c ).
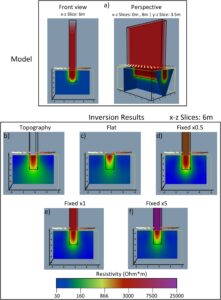
Selain penggabungan geometri model yang tepat, pertimbangan penting lain yang harus dicatat adalah penambahan informasi apriori dari parameter model, setidaknya pada bagian dinding yang terlihat, selama proses inversi. Rekonstruksi model terbaik dicapai dengan menambahkan informasi apriori dan memperbaiki resistivitas blok model dalam semua iterasi proses inversi dengan nilai yang tepat atau serupa (Gambar 7d,e ). Hasil setelah memperbaiki resistivitas blok model bagian atas dinding setengah dari yang sebenarnya (2500 Ohm*m) hampir identik dengan yang diperoleh setelah memperbaikinya ke resistivitas sebenarnya (5000 Ohm*m), menunjukkan bahwa hasil terbaik diproduksi dengan menggabungkan topografi yang tepat dalam model inversi dan membatasi parameter model ke nilai dengan resistivitas yang hampir sama. Di sisi lain, menambahkan informasi apriori, yang lima kali lebih tinggi dari nilai sebenarnya (25.000 Ohm*m), terbukti membawa bencana, menghasilkan hasil yang serupa seperti dalam kasus permukaan datar yang dijelaskan sebelumnya (Gambar 7f ).
Model lebih lanjut digunakan untuk menguji kedalaman maksimum investigasi skema pengukuran dan tata letak elektroda. Untuk pengujian ini, model sintetis yang terdiri dari blok resistif 5000 Ohm*m yang sama dengan lebar 1,5 m yang memanjang pada kedalaman 7 m digunakan (Gambar 8a ). Gambar 8b menunjukkan hasil inversi yang diperoleh dengan melakukan segmen ke- 1 , dengan pemisahan garis elektroda luar maksimum m = 1 a dan pemisahan garis elektroda dalam n = 1,5 a . Kedalaman maksimum blok model resistif berhenti pada sekitar 4 m. Penambahan pengukuran dari segmen dengan pemisahan garis elektroda luar yang meningkat memperluas kedalaman investigasi maksimum pada kedalaman yang lebih besar (Gambar 8b,c,e ). Peningkatan pemisahan garis elektroda ini menghentikan peningkatan bertahap dalam kedalaman investigasi di Segmen 3, yang sesuai dengan pemisahan garis elektroda luar maksimum m = 3 a (Gambar 8e ). Hasil serupa juga diperoleh dengan menggabungkan pengukuran segmen ke- 4 dan menambahkan pengukuran dengan pemisahan garis maksimum m = 4 a (Gambar 8f ).
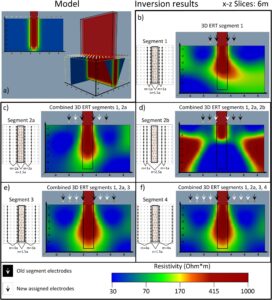
Dalam kedua kasus, hasil inversi menunjukkan bahwa blok model resistif berhenti pada kedalaman 5,5 m. Oleh karena itu, kami mendefinisikan pemisahan garis elektroda maksimum untuk geometri elektroda yang serupa pada m = 3 a , yang berhubungan dengan kedalaman investigasi maksimum.
Masalah penting yang perlu dicatat adalah peningkatan pemisahan n dari garis elektroda bagian dalam yang melekat pada blok resistif. Karena model sintetis membuktikan bahwa peningkatan pemisahan garis luar dapat meningkatkan kedalaman investigasi secara keseluruhan, peningkatan juga pemisahan garis dalam dapat memberikan hasil yang lebih baik mengenai parameter model yang lebih dalam. Gambar 8d menunjukkan hasil inversi yang diperoleh dari model yang sama dengan kombinasi Segmen 1 dan 2. Segmen 2 dibagi menjadi bagian 2a dan 2b, di mana pemisahan garis elektroda luar ditingkatkan menjadi m = 2 a . Sementara pemisahan garis elektroda bagian dalam di Segmen 2a tetap sama dengan n = 1,5 a, di Segmen 2b, ditingkatkan menjadi n = 2,5 a . Hasil inversi menunjukkan bahwa kedalaman investigasi maksimum Segmen 1 adalah sekitar 4 m dan menggabungkan data dari Segmen 1 dan 2a meningkatkan kedalaman ini menjadi 5 m. Sebaliknya, ketika pemisahan garis elektroda bagian dalam menjadi lebih besar, seperti pada Segmen 2b, dan data dari segmen ini ditambahkan ke kumpulan data gabungan dari Segmen 1 dan 2a, hasil akhir menjadi rusak. Secara keseluruhan, meningkatkan pemisahan garis elektroda bagian luar meningkatkan kedalaman investigasi, tetapi penambahan pengukuran dengan pemisahan garis elektroda bagian dalam yang lebih besar menyebabkan model yang sama sekali tidak cocok.
5 Implementasi Lapangan ERT 3D pada Tembok Bizantium Thessaloniki
Skema pengukuran yang diusulkan yang disajikan dalam karya ini telah diuji dalam kondisi nyata dan pengukuran lapangan telah dilakukan di tembok Thessaloniki, Yunani utara. Benteng tersebut telah mengalami banyak fase konstruksi, dimulai sejak abad ke-3 SM dan awalnya didirikan oleh Raja Cassander. Fase utama lainnya termasuk fase Romawi dan Ottoman yang masing-masing dimulai pada akhir abad ke-3 dan ke – 16 M , sementara pada abad ke-4 M , tembok kedua dibangun sebagai bangunan luar.
Dinding seperti yang terlihat dalam kondisi mereka saat ini terdiri dari batu bata lumpur dan batu, terutama greenschist dan marmer, diisi dengan mortar untuk membentuk agregat yang kuat. Dimensi tembok kota bervariasi dari beberapa sentimeter tingginya, menjadi sisa-sisa benteng, hingga lebih dari 5 m tinggi, dengan ketebalan berkisar dari 1 hingga 5 m. Uji skema pengukuran dilakukan di sebelah Gerbang Cassandrian baik di dinding utama dan bangunan luar. Geologi regional terdiri dari campuran endapan dan sedimen buatan termasuk tanah liat dengan kerikil dan pasir halus, sedangkan batuan dasar greenschist ditemukan pada kedalaman antara 10 dan 15 m (Panou et al. 2005 ). Untuk akuisisi data, meter resistivitas Syscal Pro dari IRIS Instruments digunakan dengan kabel multi-inti khusus.
5.1 3D ERT pada Benteng Bizantium Thessaloniki
Bagian tembok ini, yang merupakan bagian luar benteng, memiliki ketebalan 2 m dan tinggi rata-rata 0,5 m dengan sedikit variasi. Tata letak elektroda untuk kisi ERT 3D ini terdiri dari 96 elektroda, dibagi menjadi empat baris yang masing-masing terdiri dari 24 elektroda, dengan jarak 1 m di setiap elektroda dan pemisahan 1 m di antara setiap baris elektroda, sementara dua baris elektroda yang dekat dengan tembok dipisahkan oleh 2 m, menghasilkan total 3000 pengukuran (Gambar 9 ). Lebih jauh, ERT 2D dilakukan tegak lurus terhadap sumbu panjang ERT 3D menggunakan larik dipol-dipol, yang memotong kisi ERT 3D pada 8,5 m.
Untuk tujuan demonstrasi, dua inversi berbeda dilakukan, satu dengan penambahan topografi aktual dan informasi apriori pada sel model yang mewakili bagian dinding yang terlihat dan satu tanpa topografi apa pun dalam sel model. Hasil inversi menunjukkan bahwa kedalaman pondasi bangunan luar tidak melebihi 2,5 m, yang tampaknya sesuai dengan hasil yang diperoleh dengan ERT 2D (Gambar 10 ). Selain itu, anomali resistivitas rendah di dalam pondasi dinding dapat diamati di kedua hasil inversi. Area ini dapat digambarkan sebagai pondasi bangunan luar tetapi mungkin dengan kelembaban terkonsentrasi yang mengurangi resistivitas parameter model. Perlu disebutkan bahwa hasil inversi tanpa menggabungkan topografi yang tepat dalam model inversi, meningkatkan area resistivitas yang lebih rendah ini dan tampak tersebar di dalam pondasi dinding (Gambar 10a ).
5.2 3D ERT di Tembok Utama Bizantium Thessaloniki
ERT 3D kedua juga dilakukan pada dinding utama benteng. Dinding utama di bagian ini tebalnya 1,5 m dan memiliki tinggi rata-rata 0,8 m dengan variasi kecil (Gambar 11 ). Tata letak elektroda terdiri dari 96 elektroda yang dibagi dalam delapan baris yang masing-masing terdiri dari 12 elektroda dengan jarak 1 m di setiap elektroda dan pemisahan 1 m antara setiap baris elektroda sementara dua baris elektroda yang paling dekat dengan dinding dipisahkan oleh 1,5 m, memperoleh 5500 pengukuran. Sekali lagi, ERT 2D dilakukan tegak lurus terhadap sumbu panjang ERT 3D menggunakan larik dipol-dipol, memotong kisi ERT 3D pada 1 m.
Gambar 12 menunjukkan hasil inversi dengan dan tanpa menggabungkan topografi sebenarnya dalam model inversi. Pentingnya menambahkan topografi yang tepat dan membatasi parameter model selama proses inversi adalah yang terpenting, yang dapat menyebabkan interpretasi yang saling bertentangan. Hasil inversi tanpa menggabungkan topografi apa pun, membagi fondasi dalam dua zona dengan kedalaman yang sama sekali berbeda (Gambar 12a ). Di sisi lain, hasil setelah menambahkan informasi topografi dan membatasi parameter model agar sesuai dengan resistivitas dinding menghasilkan model yang lebih realistis di mana fondasi dinding utama memanjang lebih dalam daripada fondasi bangunan luar, mencapai kedalaman 3,5 m. Hasil selanjutnya juga dikonfirmasi oleh ERT 2D (Gambar 12b ).

6 Kesimpulan
Survei geolistrik dan khususnya ERT dalam ruang 2D dan 3D merupakan alat yang efektif untuk pencitraan benda-benda antik yang terkubur dan menandai fondasi dinding. Survei ini bisa sangat menantang, terutama bila diterapkan di lingkungan perkotaan dan monumen yang berdiri, karena keterbatasan ruang yang tersedia dan interaksi dengan struktur, mengingat nilai relik yang tak ternilai. Oleh karena itu, beberapa metode telah diusulkan untuk mengatasi kesulitan yang mungkin timbul dalam jenis survei ini, sekaligus meminimalkan dampak pada monumen.
Dalam karya ini, diusulkan strategi pengukuran menggunakan 3D ERT tersegmentasi, yang bertujuan untuk menggambarkan fondasi dinding atau tapak struktur geometri serupa. Tidak seperti skema serupa yang memerlukan lubang bor dan peralatan khusus untuk memperoleh resolusi yang memadai di area bawah permukaan, metode yang diusulkan dapat dicapai dengan upaya minimal, mengandalkan secara eksklusif pada elektroda permukaan dan mengukur dengan susunan pengukuran sebaris dan lintas garis sewenang-wenang yang optimal. Prospeksi yang ditargetkan diperoleh melalui proses optimasi, dengan menolak parameter model yang tidak berdekatan dengan area yang diinginkan. Resolusi pada kedalaman yang lebih besar dicapai dengan menggabungkan susunan pengukuran lintas garis dan secara bertahap meningkatkan garis elektroda aktif dari berbagai segmen 3D ERT. Namun, analisis sensitivitas menunjukkan bahwa ada batas dalam peningkatan garis elektroda ini sebelum elektroda mulai bertindak secara independen dan memisahkan parameter dari area target.
Integritas skema yang disajikan diuji dengan model sintetis yang menyerupai skenario nyata. Model maju yang direpresentasikan oleh blok model resistif yang memanjang di atas permukaan pada ketinggian yang realistis dan di bawah permukaan pada kedalaman yang rasional dapat direkonstruksi dengan mudah, yang menunjukkan keunggulan larik 3D yang dioptimalkan dibandingkan dengan larik konvensional. Karena kompleksitas geometri model dan topografi ekstrem dalam jenis survei ini, yang mencakup kemiringan hingga 90°, penggabungan geometri yang tepat dan penambahan informasi apriori ke sel model yang merepresentasikan dinding, setidaknya untuk bagian yang terlihat, selama proses inversi sangat penting untuk merekonstruksi model awal secara akurat. Model sintetis lebih lanjut dihitung untuk menguji kedalaman investigasi maksimum untuk tata letak elektroda yang serupa, serta dampak geometri dinding dalam proses inversi. Hasil menunjukkan bahwa kedalaman investigasi maksimum dengan geometri tata letak elektroda yang serupa tidak melebihi 5,5 m. Kedalaman maksimum ini dicapai dengan menggabungkan pengukuran pemisahan garis elektroda yang meningkat, tetapi sangat penting bahwa garis elektroda bagian dalam tetap melekat pada struktur.
Skema pengukuran yang diusulkan dalam studi ini digunakan untuk menyelidiki kedalaman dinding utama kuno dan fondasi bangunan luar Thessaloniki di dekat Gerbang Kassandrian. Keterbatasan instrumen menyebabkan penerapan ERT 3D yang dilakukan di segmen yang berbeda untuk melengkapi akuisisi data. Hasil inversi gabungan menunjukkan bahwa survei semacam ini mampu menggambarkan fondasi dinding secara akurat. Secara khusus, kedalaman fondasi dinding utama meluas hingga sekitar 3,5 m di bawah permukaan, sedangkan fondasi bangunan luar mencapai kedalaman 2,5 m. Lebih jauh, ERT 2D dilakukan secara tegak lurus terhadap sumbu utama monumen sebagai metode tambahan untuk memvalidasi ERT 3D. Hasil mengenai kedalaman fondasi dinding yang diperoleh dari ERT 3D tampaknya bertepatan di persimpangan tertentu.