Abstrak
Kubah Venus yang bersisi curam adalah gunung berapi melingkar selebar ∼10 km dan tinggi ∼1 km, yang dikenal karena puncaknya yang datar dan sisi-sisinya yang curam. Namun, komposisinya masih misterius. Kubah “pancake” ini kemungkinan terbentuk oleh lava dengan viskositas tinggi, dan penelitian lain telah memperkirakan berbagai komposisi, dari riolit hingga basal. Dalam penelitian ini, kami membangun pekerjaan sebelumnya yang memodelkan kubah pancake sebagai arus gravitasi viskos yang menyebar. Namun, model pembentukan kubah sebelumnya mengasumsikan bahwa mereka terbentuk di atas litosfer yang kaku. Kami sebelumnya menemukan tanda-tanda fleksur litosfer pada 14 dari 75 kubah pancake dan karena itu membangun model baru pembentukan kubah di atas litosfer elastis yang lentur. Kami menemukan bahwa fleksur selama pembentukan dapat memengaruhi bentuk kubah pancake yang dihasilkan. Hasil kami juga mendukung gagasan bahwa kubah pancake terus menyebar untuk waktu yang lama setelah penempatannya. Dalam membandingkan model kami dengan topografi kubah panekuk asli (Narina Tholus), kami menemukan berbagai viskositas lava yang tinggi, meskipun bervariasi. Kisaran viskositas lava kami terkait dengan ukuran kubah yang diamati, dan hasil kami untuk kubah besar sesuai dengan hasil penelitian lain. Kami menguji kepadatan lava yang berbeda dan menemukan bahwa kepadatan lava ∼2.400–2.700 kg/m 3 paling baik mereproduksi tanda-tanda lentur yang diamati di Narina Tholus. Lava dengan kepadatan rendah (∼1.500 kg/m 3 ) tidak mereproduksi tanda-tanda lentur, yang menyiratkan bahwa lava pembentuk kubah tidak terlalu bervesikulasi.
Poin-poin Utama
- Model kami menunjukkan bahwa fleksur mempengaruhi bentuk kubah: jika terdapat lebih banyak fleksur, bagian atas kubah akan menjadi lebih datar dan sisi-sisinya akan lebih curam.
- Kubah bertindak sebagai arus gravitasi kental yang menyebar dalam waktu lama setelah penempatannya
- Kami memperkirakan viskositas lava yang tinggi, meskipun bervariasi, dan menemukan bahwa lava dengan kepadatan lebih tinggi paling baik mereproduksi topografi yang diamati di Venus
Ringkasan Bahasa Sederhana
Venus ditutupi oleh fitur vulkanik seperti aliran panjang dan kubah datar, tetapi kita tidak tahu apakah semua vulkanisme di Venus bersifat basaltik, seperti Hawaii di Bumi. Penelitian sebelumnya tentang kubah panekuk, salah satu jenis gunung berapi di Venus, menunjukkan bahwa kubah tersebut terbentuk dari lava yang lebih lengket (lebih kental) daripada basalt biasa, berdasarkan puncaknya yang datar, sisi yang curam, dan bentuk melingkar. Untuk mempelajari tentang pembentukan dan komposisinya, kami memodelkan kubah panekuk sebagai aliran yang menyebar di atas permukaan yang melengkung di bawahnya (fleksi). Kami menemukan bahwa memasukkan fleksur memengaruhi bentuk kubah panekuk yang dimodelkan. Sisi-sisinya menjadi lebih curam, dan puncaknya menjadi lebih datar dengan adanya lebih banyak lengkungan, yang cocok dengan karakteristik visual kubah panekuk asli di Venus. Menyertakan fleksur juga memungkinkan kami untuk menguji kepadatan lava dan, karenanya, komposisinya. Model kami paling cocok dengan topografi di sekitar kubah asli menggunakan kepadatan lava yang sedikit lebih rendah daripada basalt biasa. Ini dapat menyiratkan lava yang lebih terdiferensiasi atau basalt dengan sedikit gelembung udara. VERITAS milik NASA dan EnVision milik ESA akan mengumpulkan citra beresolusi tinggi dan topografi yang akan memungkinkan kami memperluas studi ini.
1 Pendahuluan
Venus adalah keajaiban gunung berapi (misalnya, Ghail et al., 2024 ) dengan puluhan ribu aliran dan bangunan gunung berapi yang teridentifikasi (misalnya, Crumpler et al., 1997 ; Guest et al., 1992 ; Hahn & Byrne, 2023 ; Head et al., 1992 ). Mempelajari fitur-fitur ini dapat membantu kita mempelajari tentang tektonik, proses pencairan mantel, dan bahkan siklus air dari bagian dalam ke atmosfer. Sementara sebagian besar Venus ditutupi oleh dataran basaltik, pertanyaannya tetap apakah semua vulkanisme Venus bersifat basaltik. Beberapa fitur menyiratkan jenis lava yang beragam, dari canali, yang panjangnya menyiratkan lava dengan viskositas yang sangat rendah (misalnya, Kargel et al., 1994 ; Komatsu et al., 1992 ; Oshigami & Namiki, 2007 ), hingga kubah, yang sisi-sisinya yang curam menyiratkan lava dengan viskositas tinggi (McKenzie et al., 1992 ).
Kubah Venus yang bersisi curam adalah fitur vulkanik dengan radius ∼10 km dengan bentuk seperti panekuk yang khas yang komposisinya masih misterius. Kubah tersebut tingginya ∼1 km dengan sisi yang curam dan puncak yang datar. Penelitian sebelumnya telah menghubungkan morfologi ini dengan lava berkekentalan tinggi karena komposisi silikat (misalnya, Head et al., 1991 ; Pavri et al., 1992 ). Namun, yang lain berpendapat bahwa kubah panekuk kemungkinan besar bersifat basaltik atau andesit berdasarkan penelitian tentang sifat radar dan rasio aspeknya (misalnya, Bridges, 1997 ; Ford, 1994 ; Plaut et al., 2004 ; Stofan et al., 2000 ). Menemukan volume lava silika yang relatif besar di Venus akan menjadi signifikan karena di Bumi, letusan lava silika berukuran serupa sering dikaitkan dengan litosfer terhidrasi di zona subduksi, dan oleh karena itu keberadaan air dan tektonik lempeng (McKenzie et al., 1992 ). Yang lain telah berhipotesis bahwa viskositas tinggi justru dapat disebabkan oleh tingkat kristalinitas yang tinggi (Bromiley & Law, 2020 ; Cao et al., 2025 ; Sakimoto & Zuber, 1995 ) atau vesikulasi (Pavri et al., 1992 ). Dalam studi ini, kami meninjau kembali kubah Venus yang bersisi curam, yang juga disebut “kubah pancake,” untuk menjawab pertanyaan terbuka tentang pembentukan dan komposisinya.
Penelitian sebelumnya memodelkan pembentukan kubah panekuk sebagai arus gravitasi kental. Arus gravitasi kental adalah aliran yang didorong oleh gravitasi (misalnya, Huppert, 1982 ), yaitu, yang bergerak di bawah gaya beratnya sendiri (misalnya, gletser). Material dengan kepadatan lebih tinggi (dalam kasus kami, lava) mengalir horizontal melalui material dengan kepadatan lebih rendah (atmosfer Venus). McKenzie dkk. ( 1992 ) menguji model untuk dua reologi berdasarkan studi kubah silika di Bumi: fluida Bingham yang mengalir setelah tegangan luluh terlampaui (yaitu, model kaku-plastik) (Nye, 1952 ) dan fluida Newtonian (Huppert, 1982 ). Mereka membandingkan bentuk model dengan tujuh kubah panekuk dan memperkirakan viskositas lava sekitar 10 14 –10 17 Pa s (McKenzie dkk., 1992 ). Mereka menegaskan bahwa kubah kemungkinan terbentuk dari magma riolit basah. Quick et al. ( 2016 ) juga mensimulasikan penempatan kubah menggunakan model aliran volume konstan yang rileks serta aliran menyebar dengan laju injeksi lava konstan (yaitu, fluks konstan). Kedua model mengasumsikan reologi Newtonian. Mereka memperkirakan viskositas lava sekitar 10 10 –10 16 Pa s dan sekitar 10 12 –10 13 Pa s untuk model volume konstan dan fluks konstan, masing-masing. Sakimoto dan Zuber ( 1995 ) memodelkan kubah sebagai arus gravitasi kental yang mempertimbangkan komposisi dan kristalinitas. Mereka menemukan bahwa morfologi kubah dapat direproduksi dengan berbagai komposisi lava, mulai dari basaltik hingga riolitik. Namun, model pembentukan kubah sebelumnya tidak mempertimbangkan efek fleksur litosfer.
Kami sebelumnya menggunakan bukti fleksur litosfer pada kubah panekuk untuk memperkirakan ketebalan elastis di lokasinya (Borrelli et al., 2021 ). Dari 75 kubah bersisi curam yang kami identifikasi, 14 menunjukkan tanda-tanda fleksur yang dapat diatasi. Tanda-tanda ini terwujud dalam topografi sebagai kenaikan dari parit fleksur di sekitar kubah, mengarah ke tonjolan depan, dan akhirnya mendatar saat efek beban berkurang (Gambar 1 ). Mereka kemungkinan mencerminkan ketebalan elastis minimum sejak waktu pembentukan kubah (Johnson & Sandwell, 1994 ). Kami menemukan bahwa kubah panekuk dikaitkan dengan ketebalan elastis dari ∼10 hingga 40 km, kecuali yang terletak di dekat korona, yang ditemukan pada litosfer yang lebih tipis (<10 km). Hasil sebelumnya konsisten dengan hipotesis McGovern et al. ( 2013 ) bahwa gunung berapi kubah terbentuk pada litosfer dengan ketebalan menengah. Kami menunjukkan bahwa fleksur litosfer terjadi pada kubah (Borrelli et al., 2021 ), namun hingga saat ini, studi tentang pembentukan kubah hanya memodelkan kubah yang menyebar di permukaan yang kaku. Dalam studi ini, kami berusaha menjawab beberapa pertanyaan: apakah fleksur litosfer memengaruhi bentuk kubah selama pembentukan, dan jika ya, bagaimana pengaruhnya? Apa yang dapat mekanisme pembentukannya ceritakan tentang komposisinya?
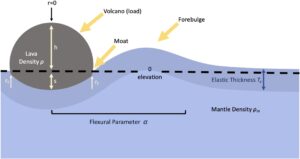
Kami memodelkan kubah panekuk sebagai arus gravitasi kental yang menyebar di atas litosfer elastis yang tertekuk. Kubah panekuk bertindak sebagai beban berat di permukaan, yang menyebabkan fleksur litosfer yang terlihat dalam topografi. Untuk mencapai ukuran kubah yang kita amati saat ini, lebih banyak lava diperlukan daripada yang dibutuhkan pada permukaan yang kaku, karena depresi fleksur di bawah kubah juga harus diisi (Gambar 1 ). Kami memperbarui model kubah sebelumnya sebagai aliran kental untuk menggabungkan efek fleksur litosfer (Borrelli et al., 2021 ). Menyertakan fleksur litosfer dalam model kami juga memungkinkan kami untuk memperkirakan kepadatan lava pembentuk kubah. Kami menguji dua reologi (Newtonian dan kaku-plastik) dan dua skenario letusan lava untuk kasus Newtonian (volume konstan dan fluks konstan). Kami akhirnya menemukan bahwa fleksur litosfer memengaruhi bentuk kubah, yang mengarah ke sisi yang lebih curam dan puncak yang lebih datar. Dengan membandingkan dengan morfologi kubah sungguhan, kami memperkirakan viskositas lava pembentuk kubah sebesar ∼10 13 –10 17 Pa s, yang sesuai dengan penelitian sebelumnya. Bentuk tanda lentur di sekitar Narina Tholus menunjukkan kisaran kepadatan lava sebesar 2.400–2.700 kg/m 3 dan tidak konsisten dengan lava yang sangat bervesikulasi dan berdensitas sangat rendah.
2 Metode
2.1 Profil Topografi Narina Tholus
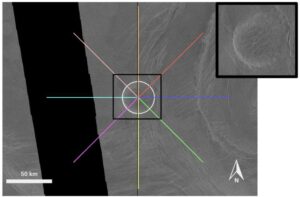
Kubah yang kami pilih untuk studi ini adalah Narina Tholus (Kubah 2 dalam Borrelli et al. ( 2021 )), yang memiliki tanda-tanda lentur yang dapat diamati. Narina Tholus adalah kandidat yang baik untuk perbandingan dengan model kami karena topografi yang diturunkan secara stereo tersedia untuk kubah ini, kubah itu sendiri dapat dipecahkan dalam topografi, dan area di sekitarnya tidak memiliki topografi tambahan yang dapat mengganggu identifikasi tanda-tanda lentur. Topografi yang diturunkan secara stereo memiliki resolusi horizontal ∼1 km dan resolusi vertikal ∼100 m (Herrick et al., 2012 ). Narina Tholus adalah satu-satunya kubah yang memiliki resolusi yang cukup untuk membedakan bentuk panekuk yang khas dan tanda-tanda lentur di sekitarnya. Narina Tholus juga telah menjadi subjek studi lentur sebelumnya. Penelitian sebelumnya menemukan ketebalan elastis yang tipis dan aliran panas permukaan yang tinggi di lokasi ini (Borrelli et al., 2021 ; Russell & Johnson, 2021 ). Dengan datangnya data beresolusi lebih tinggi dari misi mendatang, kami akan dapat memperluas studi ini ke kubah panekuk tambahan.
Kami menggunakan Java Mission-planning and Analysis for Remote Sensing (JMARS) untuk mengakses citra tampak kiri Magellan Synthetic Aperture Radar (SAR) dan topografi yang berasal dari stereo. Dengan menggunakan alat penghitung kawah JMARS dan penampil profil, kami mengumpulkan 8 profil topografi pada interval 45 derajat (Gambar 2 ). Profil dimulai di bagian tengah kubah dan memanjang ke luar sejauh 100 km. Nilai elevasi dinormalisasi menjadi 0 m pada elevasi terendah di parit lentur yang mengelilingi kubah. Semua profil di sekitar kubah ini menunjukkan tanda-tanda lentur, jadi kami merata-ratakan 8 profil untuk memperoleh satu profil radial. Model aliran Newtonian dan profil topografi kami dimulai di bagian tengah kubah. Profil topografi dicerminkan dalam gambar-gambar dalam makalah ini untuk mengilustrasikan profil kubah penuh.
2.2 Model Aliran Newtonian di Atas Litosfer yang Tertekuk
Kami mengembangkan model pembentukan kubah panekuk sebagai arus gravitasi kental di atas litosfer elastis. Penelitian sebelumnya telah memodelkan magma yang menyusup di bawah lembaran elastis (Michaut, 2011 ; Thorey & Michaut, 2014 , 2016 ) tetapi tidak mengalir di atas lapisan elastis. Derivasi persamaan untuk penyebaran arus gravitasi kental di atas litosfer kaku dalam geometri silinder dirinci dalam Huppert ( 1982 ). Model kami mencakup fleksur litosfer dan dikembangkan dalam geometri aksisimetris dari model sebelumnya yang mempelajari penebalan dan penyebaran irisan dan punggungan di margin konvergen dalam geometri kartesius (Ball et al., 2019 ; Perazzo & Gratton, 2008 ). Namun, dalam kasus kami, tidak ada istilah advektif lateral yang terkait dengan konvergensi litosfer; perpindahan litosfer hanya vertikal. Laju perubahan ketebalan kubah pancake (h − s) dapat ditulis sebagai
![]()
di mana h adalah ketebalan aliran di atas elevasi 0; s adalah deformasi litosfer (Gambar 1 ); t adalah waktu; r adalah koordinat radial dan
adalah kecepatan injeksi lava. Laju perubahan ketebalan kubah bergantung pada gravitasi ( g ), kerapatan lava (
), dan viskositas lava efektif (
). Lebih lambat untuk viskositas kubah yang lebih tinggi dan kepadatan yang lebih rendah. Arus gravitasi viskos mengalir karena beratnya sendiri, sehingga aliran yang lebih tebal ( h − s yang lebih besar ) akan bergerak lebih mudah. Model kami tidak mencakup proses variabel spasial seperti kristalinitas, blok besar, atau kerak isolasi. Untuk kesederhanaan, kami berkonsentrasi pada efek pembengkokan dan mengabaikan efek pendinginan pada viskositas lava (lih., Calusi et al., 2024 ). Model dengan efek pendinginan juga perlu mempertimbangkan efek atmosfer Venus yang tebal pada laju pendinginan lava (misalnya, Flynn et al., 2023 ; Snyder, 2002 ). Selama fase ekstrusi awal, variasi suhu terkonsentrasi di bagian depan aliran. Dalam kasus ini, ketergantungan suhu pada viskositas lava cenderung membuat kubah lebih curam (Bercovici, 1994 ). Namun, kami mempertimbangkan bentuk kubah lama setelah penempatannya, setelah kubah mendingin secara signifikan. Anomali termal kemudian berada di pusat kubah, jauh dari muka lava, dan bentuk arus gravitasi serupa dengan aliran isoviskous dengan viskositas dingin yang sesuai dengan viskositas yang dirata-ratakan pada volume kubah (Thorey & Michaut, 2016 ).
Kami menggunakan Persamaan 1 untuk memodelkan dua skenario berbeda untuk fluida Newtonian: volume konstan versus fluks konstan, seperti dalam Michaut dan Bercovici ( 2009 ). Dalam model volume konstan,
= 0 karena letusan telah berakhir. Oleh karena itu, kami memulai simulasi dengan volume lava yang terkonsentrasi di bagian tengah. Model fluks konstan mengasumsikan volume awal yang sangat kecil yang meningkat seiring dengan kecepatan injeksi lava.
karena lebih banyak lava yang meletus ke dalam aliran melalui tanggul tengah yang sempit. Istilah injeksi lava adalah
![]()
Di mana
adalah kecepatan maksimum aliran Poiseuille (aliran laminar melalui saluran silinder), dan A adalah jari-jari tanggul pengumpan silinder. Dengan mengintegrasikan Persamaan 2 di atas permukaan tanggul (dari r = 0 hingga r = A ), kita memperoleh
, di mana q 0 adalah laju injeksi lava. Dalam model ini, volume lava meningkat seiring waktu saat kubah menyebar. Kenyataannya, kubah panekuk di Venus kemungkinan terbentuk sebagai kombinasi dari skenario ini. Selama letusan, kubah akan berperilaku sesuai dengan model fluks konstan. Setelah letusan berhenti, kubah akan terus menyebar sesuai dengan model volume konstan.
Kami menggunakan model fleksur litosfer yang sudah mapan untuk menentukan perpindahan lempeng di bawahnya sebagai respons terhadap berat kubah panekuk. Seperti dalam Ball et al. ( 2019 ), model kami menggunakan persamaan fleksur dari Timoshenko dan Woinowsky-Krieger ( 1959 ). Dalam geometri asimetris, persamaan untuk deformasi litosfer elastis akibat beban vertikal adalah:

2.2.1 Nondimensionalisasi untuk Model Newtonian
Untuk mengidentifikasi parameter tak berdimensi utama yang mempengaruhi sistem dan lebih memahami fisika masalah kita, kita mennondimensionalkan Persamaan 1 dan 3 kita menggunakan tinggi karakteristik H , panjang
, dan waktu
(Tabel 1 ). Kami menggunakan subskrip v atau f untuk menunjukkan skala karakteristik yang kami gunakan untuk kasus volume konstan dan fluks konstan, masing-masing. Kami menggunakan parameter lentur
(Turcotte & Schubert, 2002 ) sebagai skala panjang karakteristik dan menghitungnya sebagai:
![]()
| Variabel | Nama | Definisi | Satuan |
|---|---|---|---|
| C | Rasio kepadatan mantel dan lava | ρmρ | tidak ada |
| Γ | Rasio parameter lentur dan radius kubah | (αrf)4 | tidak ada |
| q 0 | Laju injeksi—untuk model fluks konstan | Hfα2τf | m3 / detik |
| Ω−1 | Lebar tanggul tak berdimensi | Aα | tidak ada |
| Bahasa Indonesia: V 0 | Volume awal—untuk model volume konstan | Hvα2 | kilometer 3 |
| H dalam | Skala tinggi karakteristik—untuk model volume konstan | V0α2 | kilometer |
| H.F. | Skala ketinggian karakteristik—untuk model fluks konstan | (3μq0ρg)1/4 | kilometer |
| Hb | Skala tinggi karakteristik—untuk model plastik kaku | τyLρg | kilometer |
| H ‘ | Tinggi yang dinormalkan | jam / jam | tidak ada |
| α | Skala jarak karakteristik untuk model Newtonian | (ETe312(1−ν2)ρg)1/4 | kilometer |
| rf (rf) | Jari-jari kubah | kilometer | |
| R ‘ | Jarak yang dinormalkan—jarak tanpa dimensi | R /α | tidak ada |
| τv | Skala waktu karakteristik—volume konstan | 3α8μρgV03 | S |
| τf | Skala waktu karakteristik—fluks konstan | Hfα2q0 | S |


2.2.2 Solusi Numerik untuk Model Newtonian
Kami menghitung solusi numerik untuk Persamaan yang mengatur 9 dan 11 menggunakan metode perbedaan hingga eksplisit (lihat Lampiran A ) yang memecahkan kuantitas (h − s) dari Persamaan 9 , menghitung lentur s menggunakan Persamaan 11 , dan akhirnya menghitung h dari kedua kuantitas ini.
Untuk model volume konstan, kita mulai dengan memberi algoritma beban awal yang sesuai dengan berat kubah yang ketebalannya diberikan oleh solusi analitis di atas permukaan kaku (Persamaan 4 ). Kita menggunakan radius awal tak berdimensi kecil
, Di mana
adalah langkah ruang horizontal tak berdimensi pada grid, dan volume tak berdimensi V 0 ′ = 1. Ketebalan maksimum awal ditemukan dengan integrasi volumetrik Persamaan 4 di atas radius kubah awal, yang memberikan ketebalan awal
Selanjutnya kita hitung tekukan s yang disebabkan oleh berat beban tersebut dari Persamaan 11 , setelah itu kita dapat menghitung tinggi kubah awal di atas 0, h i .
Kami mengasumsikan pelat elastis yang lenturnya terjadi seketika selama penempatan kubah. Meskipun respons lentur sebenarnya tidak akan terjadi seketika pada tahap awal aliran kubah, kami membuat asumsi ini karena penelitian ini berfokus pada dampak lentur pada bentuk kubah lama setelah ekstrusi awal. Persamaan 9 dan 11 dipecahkan dari pusat ( r = 0), di mana kami menerapkan simetri.
, h = s = 0 karena dampak beban berkurang jauh dari kubah. Kami menggunakan kisi yang jauh lebih besar dari radius aliran dan menerapkan h = s = 0 pada ujung kisi yang lain, yaitu, tidak ada deformasi jauh dari radius aliran. Kami memverifikasi bahwa peningkatan ukuran kisi tidak mengubah hasil kami.
Kami memecahkan h dan s pada grid penuh, dan memverifikasi bahwa mengubah panjang grid atau ukuran langkah ruang
tidak memengaruhi hasil kami. Kami juga memverifikasi kekekalan massa, yaitu, bahwa volume aliran memang tetap konstan seiring waktu.
Untuk model fluks konstan, kita memilih volume awal dan tinggi kecil h 0 = 0,1. Kita mulai dengan radius tanggul tak berdimensi
Di luar tanggul ( r >
), laju injeksi lava adalah 0. Metode penyelesaian numerik untuk model fluks konstan sama dengan model volume konstan, selain dari nilai laju injeksi lava. Kami memverifikasi konservasi massa dengan mengikuti peningkatan volume seiring waktu untuk model fluks konstan.
2.3 Model Aliran Plastik Kaku di Atas Litosfer yang Tertekuk
Seperti dalam McKenzie et al. ( 1992 ), kami juga menguji model quasi-statis untuk pembentukan kubah panekuk menggunakan reologi Bingham berdasarkan model yang dikembangkan oleh Nye ( 1952 ) untuk gletser. Dalam kasus di mana kubah plastik kaku menyebar di atas permukaan yang dapat bergerak vertikal dengan menekuk, persamaan quasi-statis menjadi:

2.3.1 Non-Dimensionalisasi untuk Model Plastik Kaku
Dalam kasus ini, kubah memiliki radius tetap dan integrasi Persamaan 13 menghasilkan bentuk kuasi-statis kubah. Oleh karena itu, kami men-nondimensionalkan Persamaan 13 kuasi-statis dengan menggunakan radius kubah r f sebagai panjang karakteristik dan tinggi karakteristik H b :

3 Hasil
3.1 Perubahan Bentuk Kubah Seiring Bertambahnya Radius
Model kubah panekuk kami sebagai arus gravitasi kental memungkinkan kami melacak bentuk kubah seiring waktu. Dalam model volume konstan Newtonian, volume lava tertentu secara instan ditempatkan dan terkonsentrasi di pusat grid (Gambar 3a ). Beban relatif tinggi dan sempit pada langkah waktu awal sebelum kubah menyebar, dan ada pembengkokan signifikan di bawah beban. Seiring berjalannya waktu, kubah menyebar secara radial ke luar, menjadi lebih pendek dan lebih lebar. Depresi lentur litosfer juga melebar dan menjadi lebih dangkal di bagian tengah saat beban didistribusikan ke area yang lebih luas. Dalam model fluks konstan Newtonian, lava meletus pada laju konstan dari tanggul pusat yang sempit (Gambar 3b ). Volume kubah pada langkah waktu awal kecil, dan terkonsentrasi di bagian tengah sebagai beban tinggi dan sempit. Karena bebannya kecil, depresi lentur dapat diabaikan di awal. Seiring dengan semakin banyaknya lava yang meletus, volume kubah meningkat dan menyebar secara radial ke luar, menyebabkan semakin banyaknya lipatan litosfer.
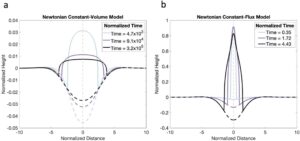
Model kubah yang kami buat di atas litosfer yang melengkung menghasilkan bentuk yang berbeda dari model kubah yang dibuat di atas litosfer yang kaku dan datar. Kami membandingkan bentuk kubah menggunakan model aliran viskos Newtonian kami di atas litosfer yang melengkung dengan solusi litosfer kaku dari Huppert ( 1982 ) (Gambar 4 ) dan Nye ( 1952 ). Parameter lentur terkait dengan ketebalan elastis dan kekakuan lentur,
, di mana litosfer yang lebih tebal sesuai dengan kekakuan lentur yang lebih tinggi, dan karenanya deformasi yang lebih sedikit. Ketika radius kubah jauh lebih kecil daripada parameter lentur, lentur litosfer dapat diabaikan, dan bentuk kubah sesuai dengan solusi litosfer kaku karena kubah terbentuk di atas permukaan yang berperilaku serupa dengan permukaan kaku. Namun, ketika radius kubah lebih besar daripada parameter lentur, lenturan menjadi signifikan, dan bentuk kubah berbeda dari solusi kesamaan Huppert ( 1982 ). Dengan menggunakan model Newtonian volume konstan, kubah yang terbentuk di atas litosfer yang lentur akan mengembangkan sisi yang lebih curam dan puncak yang lebih datar daripada yang ada di atas litosfer kaku (Gambar 4 ).

3.2 Model Mereproduksi Topografi Kubah Pancake yang Diamati
Model kami mereproduksi topografi kubah panekuk di Venus (Gambar 5 ). Kami mengukur kesesuaian untuk model Newtonian volume konstan dan model plastik kaku dibandingkan dengan topografi kubah aktual (Gambar 5 ). Model Newtonian hanya bergantung pada C , sedangkan model plastik kaku bergantung pada C dan
Namun, dalam model dinamis Newtonian, jari-jari aliran tak berdimensi (
) meningkat, yang setara dengan perubahan
dalam kasus plastik kaku statis. Kami sebelumnya menemukan bahwa kubah sering terbentuk di tempat litosfer memiliki ketebalan ∼15–40 km, atau di tempat parameter lentur
adalah ∼30–80 km (Borrelli et al., 2021 ). Beberapa kubah terletak di dekat korona, dan ditemukan di mana ketebalan elastisnya <10 km. Di Narina Tholus, parameter lenturnya adalah ∼12 km dan radiusnya ∼20 km. Untuk tujuan perbandingan ini, kami menunjukkan simulasi kami di mana radius tak berdimensinya adalah
untuk model Newtonian, yang sesuai dengan
untuk model kaku-plastik. Kami mengukur kesesuaian dengan terlebih dahulu memperkirakan perbedaan positif antara model dan topografi yang diamati menggunakan
![]()
Kami kemudian mengintegrasikan ketidaksesuaian ini ke bentuk cakram dari r = 0 hingga r = 100 km menggunakan
![]()
di mana R = 100 km.
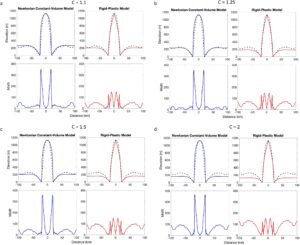
Kuantifikasi kami terhadap kecocokan model lebih baik untuk model volume konstan Newtonian dalam semua kasus (Tabel 2 ). Model Newtonian mampu mereproduksi fleksur litosfer yang diamati, sementara model kaku-plastik menunjukkan fleksur yang terlalu sedikit dalam semua kasus (Gambar 5 ). Kami mengasumsikan kompensasi total berat kubah oleh fleksur, meskipun ini masih dapat berlangsung karena viskositas mantel yang besar. Lokasi kesalahan terbesar sepanjang profil kubah memberikan hasil yang menarik: sementara kesalahan yang lebih besar terletak di sepanjang sisi kubah dalam kasus Newtonian, itu lebih besar di bagian dalam kubah dan topografi sekitarnya dalam kasus kaku-plastik. Kesalahan besar pada sisi dalam kasus Newtonian dapat menunjukkan bahwa lereng curam yang diprediksi oleh model tidak berkelanjutan dalam skala waktu yang panjang, dan kubah mungkin telah terkikis sejak pembentukannya. Seperti dicatat oleh Nye ( 1952 ), model kaku-plastik tidak akurat di bagian tengah grid, di mana ia membentuk diskontinuitas dalam profil. Hal ini tampak sebagai puncak yang runcing, sedangkan puncak kubah seharusnya datar karena simetri sekitar r = 0. Akan tetapi, model plastik kaku ini tidak menghasilkan puncak datar khas kubah panekuk Venus.
| C | Kesalahan volume konstan Newtonian | Kesalahan plastik kaku |
|---|---|---|
| 1.1 | 31.23 | 34.75 |
| 1.25 | 19.48 | 50.47 |
| 1.5 | 35.81 | 73.19 |
| 2 | 72.92 | 103.34 |
Secara visual, dan seperti yang dilaporkan oleh McKenzie et al. ( 1992 ), kami menemukan bahwa model aliran Newtonian volume konstan paling baik mereproduksi bentuk “pancake” khas kubah. Ini selanjutnya didukung oleh lokasi kesalahan terbesar di seluruh profil (Gambar 5 ). Model Newtonian fluks konstan mengembangkan tonjolan di bagian tengahnya dalam skala waktu yang panjang karena kubah menyebar lebih lambat daripada lava yang terakumulasi di atas tanggul (Gambar 3 ). Model plastik kaku memprediksi kemiringan yang lebih konstan di sisi kubah, sisi yang kurang curam, dan tidak menunjukkan karakteristik puncak datar dari kubah panekuk. Model Newtonian volume konstan menunjukkan fitur karakteristik kubah panekuk, puncak datar dan sisi yang sangat curam, bahkan dalam skala waktu yang panjang. Ia juga mereproduksi tanda-tanda lentur di sekitar kubah, sedangkan model plastik kaku tidak menyebabkan cukup lentur untuk mereproduksi topografi yang diamati. Dengan demikian, model Newtonian tampaknya merupakan perkiraan bentuk kubah yang lebih baik. Oleh karena itu kami menggunakan skenario volume konstan Newtonian dalam analisis kami mengenai perkembangan aliran kubah.
3.3 Dampak Kepadatan Lava terhadap Bentuk Kubah
Pilihan kerapatan lava merupakan pertimbangan penting, karena memiliki efek signifikan pada respons lentur litosfer di sekitarnya. Kami menguji hipotesis bahwa lava pembentuk kubah dapat memiliki kerapatan rendah karena sangat vesikulasi, meskipun kami tidak mengecualikan sejumlah kecil vesikulasi. Karena C adalah rasio kerapatan lava terhadap kerapatan mantel, pilihan kerapatan mantel kami memengaruhi kerapatan yang kami uji. Misalnya, nilai C = 1,1 (Gambar 5a ) dapat sesuai dengan kerapatan lava 2.700 kg/m3 dan kerapatan mantel 3.000 kg/ m3 . Ini mungkin sesuai dengan andesit atau basal dengan vesikulasi ~10% (Bridges, 1997 ). Kami juga menguji nilai C = 1,25, C = 1,5 dan C = 2, yang sesuai dengan kepadatan lava sebesar 2.400, 2.000, dan 1.500 kg/m 3 , masing-masing, menggunakan kepadatan mantel yang sama. Kepadatan lava sebesar ∼2.400 kg/m 3 mensimulasikan riolit cair dalam kondisi Venus (Shellnutt, 2013 ) atau basal dengan ∼20% vesikulasi (Bridges, 1997 ). Kepadatan lava sebesar 1.500 kg/m 3 mensimulasikan lava yang harus sangat vesikulasi, terlepas dari komposisinya. Mengingat viskositas tinggi dan skala waktu penyebaran yang panjang dari simulasi model kami, lava pembentuk kubah sebagian besar akan menjadi padat, dan dengan demikian lebih padat daripada nilai yang diharapkan untuk lava cair. Kami juga mencatat bahwa kepadatan untuk basal Venus di Bridges ( 1997 ) mengasumsikan keberadaan air dan kandungan volatil mirip Bumi. Kami menemukan bahwa pilihan kepadatan lava tidak berdampak pada bentuk kubah itu sendiri, tetapi mengubah bentuk tanda lentur di sekitarnya (Gambar 6 ). Model memberikan kecocokan terbaik dengan topografi yang diamati menggunakan C = 1,1 dan C = 1,25, sementara C ≥ 1,5 tidak menghasilkan beban yang cukup untuk mencocokkan topografi yang diamati (Gambar 5 ).

3.4 Viskositas dan Skala Waktu Penyebaran
Kami menggunakan model aliran Newtonian fluks konstan untuk memperoleh hasil yang berdimensi untuk viskositas lava dan skala waktu penyebaran. Kami menggunakan model fluks konstan karena rezim ini mensimulasikan lava yang meletus dan selama itu kubah mencapai ketinggian maksimumnya. Setelah letusan berakhir, kubah menyebar sebagai aliran volume konstan, dan ketinggiannya berkurang seiring waktu. Kubah bisa saja lebih tinggi sebelum memasuki rezim volume konstan dan mencapai ketinggian kubah yang kita lihat sekarang. Oleh karena itu, estimasi kami untuk viskositas menggunakan model fluks konstan adalah minimum. Kami mengambil rasio ketinggian maksimum yang diamati dari Narina Tholus dibandingkan dengan ketinggian tak berdimensi maksimum dari profil yang kami modelkan, dan melakukan hal yang sama untuk radius. Rasio ini berfungsi sebagai masukan untuk H f dan
(Tabel 3 ). Kita kemudian dapat mengatur ulang definisi H f untuk menyelesaikan viskositas
menggunakan berbagai laju injeksi dari 0,1 hingga 1.000 m 3 /s. Kami juga memecahkan persamaan untuk
, dan kalikan nilai ini dengan waktu model tak berdimensi untuk menentukan skala waktu penyebaran.
| Konstan | Definisi | Nilai | Satuan |
|---|---|---|---|
| q0 | Fluks/laju injeksi konstan | 0,1–1.000 | m3 / detik |
| ρ | Kepadatan lava | 1.500–2.700 | kg/ m3 |
| ρm | Kepadatan mantel (Johnson & Sandwell, 1994 ) | 3.000 orang | kg/ m3 |
| α=(ETe312(1−ν2)ρg)1/4 | Parameter lentur pada Narina Tholus | 12 | kilometer |
| T | Penyebaran skala waktu | 30–3 × 10 5 | Tahun Bumi |
| μ | Kekentalan lava | 10 13 –10 17 | Pas |
Hasil kami sangat bergantung pada pilihan laju injeksi lava ( q0 ) , dan ketinggian kubah. Kami menguji rentang q0 dari 0,1 hingga 1.000 m3 / detik , dengan nilai q0 yang lebih tinggi menghasilkan viskositas yang lebih rendah. Rentang ini didasarkan pada laju efusi di Bumi (Harris et al., 2007 ), yang dapat sangat bervariasi (Michaut et al., 2013 ) dan sulit diukur (Garel et al., 2013 ). Batas atas rentang ini mendekati laju maksimum selama letusan Laki (∼8,7 × 103 m3 / detik ) , salah satu aliran lava terbesar dalam sejarah terkini (Thordarson & Self, 1993 ). Kami menggunakan simulasi fluks konstan di mana
Dan
. Kami menemukan viskositas lava yang besar, tetapi bervariasi. Di Narina Tholus, yang relatif tinggi, kami menemukan viskositas lava pembentuk kubah sebesar ∼10 13 –10 17 Pa s. Secara keseluruhan, kami menemukan skala waktu penyebaran sebesar ∼30–300.000 tahun Bumi.
4 Diskusi
4.1 Kubah Menyebar Lama Setelah Penempatan
Aplikasi model kami pada Narina Tholus menunjukkan bahwa kubah panekuk dapat terus menyebar lama setelah penempatannya. Skala waktu penyebaran yang kami perkirakan untuk kubah ini menggunakan model Newtonian fluks konstan jauh lebih lama daripada durasi letusan yang wajar (hingga ratusan ribu tahun Bumi). Skala waktu yang panjang ini cukup untuk memungkinkan akomodasi berat kubah oleh pembengkokan litosfer dan aliran astenosfer. Ini konsisten dengan studi terbaru yang memodelkan kubah sebagai arus gravitasi kental yang dialiri oleh celah yang tidak berbentuk silinder sempurna, dan menemukan bahwa kubah membutuhkan waktu lama untuk menjadi lingkaran sempurna (Mériaux et al., 2022 ). Hasil mereka menunjukkan bahwa letusan lava di kubah panekuk dapat berlangsung dari ∼8 hingga 140 tahun Bumi (Mériaux et al., 2022 ). Hasil kami tidak membedakan antara waktu yang dihabiskan dalam rezim fluks konstan versus volume konstan, dan hanya memberikan waktu total untuk letusan kubah menggunakan model fluks konstan. Setelah letusan berhenti, kubah terus menyebar sebagai aliran volume konstan selama sebagian besar waktu pembentukannya. Suhu permukaan Venus yang tinggi memungkinkan kubah menyebar dalam rentang waktu yang lebih panjang. Hasil kami mendukung mekanisme pembentukan ini karena model aliran Newtonian volume konstan memberikan kecocokan terbaik dengan topografi kubah yang diamati. Saat kubah mendingin selama rezim penyebaran volume konstan, viskositas efektifnya meningkat. Perkiraan kami untuk viskositas lava dan rentang waktu penyebaran menggunakan model fluks konstan adalah minimum.
Beberapa kubah juga dapat ditempatkan secara episodik, dalam hal ini transisi dari aliran fluks konstan ke aliran volume konstan akan terjadi beberapa kali. Fink et al. ( 1993 ) melakukan eksperimen laboratorium yang menciptakan kubah lilin dan menentukan bahwa rasio aspek kubah yang dibentuk oleh beberapa episode penempatan lebih cocok dengan pengamatan kubah panekuk tertentu. Kubah yang dibentuk oleh beberapa episode memiliki rasio aspek yang lebih tinggi (tinggi/diameter) daripada yang dibentuk oleh letusan tunggal yang berkelanjutan. Gleason et al. ( 2010 ) menggunakan topografi yang berasal dari stereo untuk menemukan bukti penempatan episodik di beberapa kubah. Mereka mengidentifikasi dua kubah yang tampaknya memiliki beberapa lobus, yang menunjukkan beberapa peristiwa letusan, termasuk Narina Tholus. Mereka menyimpulkan bahwa Narina Tholus mungkin telah terbentuk di atas fitur yang lebih tua, dan kemungkinan besar terbentuk karena beberapa peristiwa letusan. Namun, Pavri et al. ( 1992 ) melakukan survei terhadap kubah dan menentukan bahwa mayoritas kemungkinan terbentuk dari satu peristiwa letusan tunggal daripada secara episodik seperti kubah serupa yang terbentuk di Bumi. Di masa mendatang, pemodelan penempatan kubah sebagai beberapa letusan episodik dapat memberikan wawasan tentang pembentukan (setidaknya beberapa) kubah panekuk.
4.2 Dampak Fleksur Litosfer terhadap Bentuk Kubah
Model baru kubah panekuk kami yang menyebar di atas litosfer yang tertekuk berfungsi sebagai pembaruan untuk studi sebelumnya yang memodelkan kubah sebagai arus gravitasi kental di atas litosfer yang kaku (misalnya, McKenzie et al., 1992 ; Quick et al., 2016 ; Sakimoto & Zuber, 1995 ). Model kami memberikan simulasi pembentukan kubah yang lebih akurat karena memperhitungkan efek fleksur, yang telah kami konfirmasi terjadi pada 14 dari 75 kubah panekuk (Borrelli et al., 2021 ).
Hasil kami menunjukkan bahwa pembengkokan litosfer memang berdampak pada bentuk kubah, khususnya untuk kubah yang terbentuk di atas litosfer yang lebih tipis. Pembengkokan litosfer menghambat pergerakan lava, suatu efek yang tidak terjadi pada permukaan yang datar dan kaku. Ketika radius kubah sama dengan atau lebih besar dari parameter lentur, bentuk kubah berbeda dari solusi analitis kubah yang terbentuk di atas litosfer yang kaku. Dengan menggunakan model kaku-plastik, sisi kubah menjadi lebih curam ketika terdapat lebih banyak lenturan litosfer. Untuk fluida Newtonian, bagian atas menjadi lebih datar dan sisi-sisinya menjadi lebih curam. Tekanan hidrostatik dalam aliran mendorong arus gravitasi. Gradien tekanan hidrostatik perlu ditingkatkan agar bagian depan lava dapat terus menyebar bahkan ketika litosfer membengkok di sekitarnya. Ketika radius kubah tumbuh, bentuknya semakin menyimpang dari solusi litosfer yang kaku. Model teoritis kami memprediksi perubahan kemiringan dan dengan demikian morfologi kubah dengan meningkatnya radius kubah dan parameter lenturan. Kami belum dapat menguji prediksi ini menggunakan data topografi yang tersedia, tetapi misi masa depan akan memberikan kesempatan ini.
4.3 Lava Pembentuk Kubah Memiliki Viskositas dan Kepadatan Tinggi
Kami menemukan bahwa lava pembentuk kubah memiliki viskositas efektif yang tinggi. Hasil kami sebesar ∼10 13 –10 17 Pa s serupa dengan hasil penelitian sebelumnya. McKenzie et al. ( 1992 ) menemukan viskositas lava sebesar ∼10 14 –10 17 Pa s, dan Quick et al. ( 2016 ) menemukan viskositas sebesar ∼10 10 –10 16 Pa s dan ∼10 12 –10 13 Pa s tergantung pada model yang digunakan. Model aliran Newtonian kami untuk Narina Tholus menggunakan lava dengan kepadatan lebih tinggi memberikan kesesuaian terbaik dengan data. Estimasi viskositas kami untuk skenario ini berada dalam kisaran viskositas yang ditemukan oleh McKenzie et al. ( 1992 ) dan Quick et al. ( 2016 ). Viskositas lava terkait dengan tinggi kubah. Beberapa kubah lebih pendek (<200 m tinggi) daripada Narina Tholus (>1 km tinggi). Viskositas lava yang kami perkirakan dari kubah yang lebih pendek akan lebih kecil daripada estimasi yang kami harapkan untuk kubah yang jauh lebih tinggi, pada urutan 10 9 –10 13 Pa s. Baik McKenzie et al. ( 1992 ) dan Quick et al. ( 2016 ) membandingkan model mereka dengan kubah besar (>1 km tinggi), membuat hasil mereka mirip dengan hasil kami untuk Narina Tholus. McKenzie et al. ( 1992 ) menyimpulkan bahwa hanya riolit yang akan memiliki viskositas yang cukup tinggi untuk membentuk kubah panekuk tanpa mendingin terlalu cepat. Mereka juga mencatat bahwa di Bumi, letusan besar lava silika paling sering terjadi di zona subduksi dan karena itu terkait dengan keberadaan air (McKenzie et al., 1992 ). Ketika memperhitungkan kerak isolasi di atas aliran, Quick et al. ( 2016 ) berpendapat bahwa andesit basal merupakan komposisi yang paling memungkinkan untuk kubah panekuk.
Penelitian sebelumnya memperkirakan komposisi lava pembentuk kubah dan kristalinitas. Bromiley dan Law ( 2020 ) menyajikan model untuk pembentukan kubah berdasarkan pengamatan bentuk lahan vulkanik di Siprus di mana kubah terbentuk melalui letusan episodik dari “bubur” yang sangat mengkristal. Cao et al. ( 2025 ) menggunakan komposisi massal dari Venera 13 dan 14 untuk memperkirakan viskositas lava dalam skenario yang berbeda. Mereka menemukan bahwa viskositas lava pada urutan yang diharapkan untuk kubah panekuk memerlukan fraksi kristal yang sangat tinggi (>50%), yang memerlukan proses magmatik yang tidak biasa. Model oleh Sakimoto dan Zuber ( 1995 ) mereproduksi morfologi kubah menggunakan berbagai komposisi lava (termasuk basal, andesit, dan riolit) dan kandungan kristal. Mereka akhirnya menyimpulkan bahwa kubah panekuk belum tentu merupakan bukti vulkanisme silikat di Venus dan bahwa morfologi kubah saja tidak dapat digunakan untuk menunjukkan komposisinya.
Hasil kami menyiratkan bahwa lava pembentuk kubah tidak terlalu vesikular, dan komposisinya tidak dapat dibatasi. Model aliran Newtonian kami menggunakan kepadatan lava yang sangat rendah tidak memberikan beban yang cukup untuk menghasilkan tanda-tanda lentur pada topografi sekitar Narina Tholus. Kami menguji kepadatan lava ∼1.500 kg/m 3 untuk mensimulasikan riolit dengan volume gelembung ∼30% (Bridges, 1997 ) atau basal dengan volume gelembung ∼45% (Pavri et al., 1992 ). Pavri et al. ( 1992 ) menguji model kenaikan magma di mana eksolusi volatil dalam lava basaltik dapat menyebabkan lava dengan kandungan gelembung tinggi dan viskositas tinggi. Tergantung pada konsentrasi CO 2 dalam magma, lava dengan kepadatan sekitar 600–2.000 kg/m 3 dan fraksi volume gelembung hingga sekitar 75% dapat meletus dalam kondisi Venus (Pavri et al., 1992 ). Kepadatan terendah yang kami uji adalah perkiraan yang wajar untuk lava yang sangat bervesikulasi dalam kisaran fraksi volume gelembung yang mungkin dalam kondisi Venus tanpa memerlukan letusan eksplosif (Pavri et al., 1992 ). McKenzie et al. ( 1992 ) mencatat bahwa satu-satunya kubah lava di Bumi yang volumenya sebanding dengan kubah panekuk Venus berada di kaldera Yellowstone, dengan volume sekitar 75–200 km 3 . Namun, jika lava pembentuk kubah memiliki konsentrasi gelembung yang tinggi, total volume magma yang diperlukan untuk membentuk kubah secara signifikan lebih rendah daripada yang diharapkan untuk lava yang lebih padat (Pavri et al., 1992 ). Kami menguji hipotesis bahwa konsentrasi tinggi gelembung dalam lava pembentuk kubah, yang dimungkinkan oleh tekanan permukaan yang tinggi, mungkin menjadi alasan bahwa kubah lava besar lebih umum di Venus daripada di Bumi (McKenzie et al., 1992 ; Pavri et al., 1992 ). Pada akhirnya, kami menemukan bahwa lava dengan kepadatan lebih tinggi (∼2.400–2.700 kg/m 3 ) memberikan kecocokan terbaik dengan topografi yang diamati di Narina Tholus. Hasil kami menyiratkan bahwa lava pembentuk kubah tidak terlalu bervesikulasi. Model mereproduksi topografi menggunakan kepadatan lava yang diharapkan dari andesit dan riolit dalam kondisi Venus (Shellnutt, 2013 ), jadi kami tidak dapat mengesampingkan komposisi apa pun. Kami juga tidak mengesampingkan basal dengan jumlah vesikulasi yang lebih kecil (<20%).
5 Kesimpulan
Kami mengembangkan model baru arus gravitasi kental di atas litosfer elastis yang tertekuk. Kami menerapkan model ini ke kubah panekuk di Venus (Narina Tholus) dan menemukan bahwa fleksur selama pembentukan memengaruhi bentuk kubah, mungkin menjadi kunci ciri khas puncak datar dan sisi curamnya. Kami menemukan bahwa lava pembentuk kubah memiliki viskositas tinggi, sesuai dengan McKenzie et al. ( 1992 ) dan Quick et al. ( 2016 ). Model kami tidak mereproduksi ciri khas fleksur di sekitarnya saat kerapatan lava sangat rendah, yang menyiratkan bahwa lava pembentuk kubah tidak terlalu bervesikulasi. Kami menemukan bahwa kerapatan lava ∼2.400–2.700 kg/m 3 memberikan kesesuaian terbaik dengan topografi yang diamati. Riolit atau andesit Venus cair memiliki kerapatan di ujung bawah kisaran ini (Shellnutt, 2013 ). Namun, saat kubah panekuk terbentuk dalam jangka waktu yang panjang, kubah tersebut akan mengeras dan kepadatan lava pembentuk kubah akan meningkat. Kepadatan ini juga dapat dihasilkan oleh batuan basalt dengan beberapa vesikulasi (Bridges, 1997 ). Dengan demikian, kita tidak dapat mengesampingkan salah satu dari ketiga komposisi ini. Pekerjaan di masa mendatang harus menguji model penempatan kubah menggunakan peristiwa letusan episodik yang berbeda. Pekerjaan di masa mendatang juga harus menentukan jumlah waktu yang dihabiskan di bawah rezim fluks konstan dan volume konstan untuk satu kubah dan kapan transisi antara keduanya terjadi.
Model yang kami kembangkan dalam karya ini dapat membantu kami menentukan komposisi kubah panekuk, tetapi saat ini kami hanya menerapkannya pada satu kubah karena resolusi topografi dan pencitraan yang tersedia rendah. Namun, misi masa depan ke Venus akan memungkinkan kami untuk menerapkan model kami ke seluruh populasi kubah panekuk. Misi VERITAS (Emisi Venus, Ilmu Radio, InSAR, Topografi, dan Spektroskopi) NASA yang akan datang dan misi EnVision ESA ke Venus akan mengumpulkan data resolusi lebih tinggi yang dapat meningkatkan pemahaman kita tentang kubah panekuk. VERITAS akan mengumpulkan citra global pada resolusi <30 m dan topografi lebih dari ∼95% permukaan dengan resolusi horizontal ∼300 m dan resolusi vertikal <10 m (Widemann et al., 2023 ). EnVision akan mengumpulkan citra radar di wilayah tertentu dengan resolusi ∼10–30 m, dan topografi pada resolusi horizontal ∼300 m dan resolusi vertikal ∼20 m (Widemann et al., 2023 ). Citra dan topografi baru ini akan mengungkap tanda-tanda lentur di sekitar lebih banyak kubah. Kita juga akan mengatasi perbedaan yang lebih halus dalam morfologi kubah dan melihat tren yang memberi kita lebih banyak informasi tentang pembentukannya. Saat kita memulai “dekade Venus”, kita dapat memperluas studi ini menggunakan data resolusi tinggi untuk lebih banyak kubah saat tersedia.
