Kombinasi konsisten antara mikrofisika dua momen dan sifat optik es curah, serta dampaknya terhadap radiasi dalam model cuaca regional

Abstrak
Kami menyajikan kopling konsisten antara mikrofisika dua momen dan optik es massal dalam model cuaca regional resolusi 1,5 km milik Met Office dan mempelajari dampaknya pada iradiasi gelombang pendek dan panjang di puncak atmosfer (TOA). Kopling tersebut menghubungkan momen prognostik (massa total dan jumlah) dengan sifat optik es massal melalui radius bola ekuivalen massa menggunakan aproksiman Padé. Model dijalankan dievaluasi untuk Darwin, Australia (Januari–Maret 2017) dan Inggris (Desember 2017–Maret 2018). Dengan menggunakan parameterisasi kopling konsisten ini, kami menunjukkan simulasi iradiasi gelombang pendek TOA yang lebih baik di kedua wilayah dibandingkan dengan parameterisasi optik es yang tidak konsisten saat divalidasi terhadap pengamatan satelit. Peningkatan serupa ditemukan untuk iradiasi gelombang panjang TOA di Darwin, meskipun parameterisasi konsisten sedikit terlalu transmisif di Inggris. Secara keseluruhan, penggabungan dua momen yang lebih konsisten antara mikrofisika dan optik es mengarah pada prediksi medan radiasi yang secara umum lebih baik daripada parametrisasi momen tunggal.

1. PENDAHULUAN
Panel Antarpemerintah tentang Perubahan Iklim (IPCC) telah lama menyoroti kurangnya pemahaman tentang kopling radiatif awan ke atmosfer, terutama dalam laporan 2021 mereka dan penilaian sebelumnya. Kesenjangan dalam pengetahuan ini memperburuk ketidakpastian yang signifikan dalam memprediksi keseimbangan iklim Bumi, seperti yang dirangkum oleh Stocker et al . ( 2013 ). Penggerak utama ketidakpastian ini adalah efek umpan balik radiatif awan, seperti yang dibahas oleh Boucher et al . ( 2013 ) dan Sherwood et al . ( 2020 ). Ketidakpastian ini sebagian muncul dari asumsi fisika awan yang berbeda dalam berbagai model yang digunakan untuk penilaian IPCC dan terkait erat dengan bias saat ini dalam sifat awan yang diprediksi oleh model iklim, lihat misalnya Rostron et al . ( 2020 ), Ceppi dan Nowack ( 2021 ), Furtado et al . ( 2023 ), dan Jiang et al . ( 2023 ).

Awan kristal es, atau cirrus, berkontribusi signifikan terhadap ketidakpastian dalam tanda umpan balik radiatif. Awan ini dapat mendinginkan atau menghangatkan permukaan planet tergantung pada keadaan makrofisika dan mikrofisika mereka (Baran, 2012 ; Liou, 1986 ; Yang et al ., 2015 ; Zhang et al ., 1999 ). Secara keseluruhan, awan cirrus diamati berkontribusi pada efek pemanasan bersih sekitar 5,1 ± 3,1 W m −2 (Hong et al ., 2016 ). Namun, nilai ini memiliki ketidakpastian yang signifikan karena perbedaan perlakuan distribusi ukuran partikel kristal es (PSD) dan kebiasaan kristal es dalam pengambilan satelit yang digunakan untuk memperkirakan efek radiatif bersih cirrus.

Perbedaan-perbedaan dalam mikrofisika cirrus ini juga terwujud dalam model-model yang digunakan dalam penilaian IPCC, yang berkontribusi pada perbedaan antarmodel yang disebutkan sebelumnya. Lebih jauh lagi, mikrofisika dan parameterisasi radiatif cirrus dalam model-model dapat memengaruhi prediksi awan rendah karena profil vertikal pemanasan, seperti yang ditunjukkan oleh McFarquhar et al . ( 2003 ). Proses hamburan dan penyerapan oleh kristal-kristal es atmosfer sangat penting untuk profil vertikal pemanasan dalam cirrus (Yang et al ., 2012 ; Zhao et al ., 2018 ) dan untuk sifat-sifat radiatif gelombang pendek dan gelombang panjang mereka (Baran, 2009 ; Yang et al ., 2015 ). Akan tetapi, tergantung pada model kristal es yang diadopsi untuk sifat-sifat hamburan dan penyerapan, mungkin ada perbedaan substansial untuk simulasi radiatif cirrus dalam model-model sirkulasi umum (GCM) dan untuk pengambilan sifat-sifat cirrus dari satelit; lihat misalnya karya-karya Edwards et al . ( 2007 ), Yang dkk . ( 2012 ), Yang dkk . ( 2013 ), Baran, Hill, dkk . ( 2014b ), Zhao dkk . ( 2018 ), Ren dkk . ( 2021 ), dan Ren dkk . ( 2023 ).

Untuk mengukur dan membatasi efek radiatif bersih dari cirrus, sangat penting untuk membuat parametrisasi akurat dari sifat optik massal mereka. Namun, seperti yang telah ditunjukkan oleh banyak penelitian, belum ada konsensus tentang model kristal es dari sifat optik es massal mana yang paling baik untuk diterapkan dalam GCM dan/atau penginderaan jarak jauh. Mengingat berbagai model hamburan yang ada (lihat misalnya Baran, Cotton, et al ., 2014a ; Baum et al ., 2011 ; Eriksson et al ., 2018 ; Kleanthous et al ., 2024 ; Li et al ., 2022 ; Yang et al ., 2013 ), memastikan beberapa tingkat konsistensi antara mikrofisika GCM dan skema radiasi sangat penting. Ini biasanya dicapai dengan memastikan bahwa PSD, dimensi massa model kristal es, atau dimensi karakteristik PSD konsisten antara dua skema (Bae et al ., 2016 ; Baran et al ., 2016 ; Baran, Hill, et al ., 2014b ; Ren et al ., 2021 ; Ren et al ., 2023 ; Zhao et al ., 2018 ). Studi terbaru oleh Ren et al . ( 2023 ) menekankan pentingnya konsistensi dalam model optik awan es ketika diterapkan pada penginderaan jarak jauh dan simulasi perpindahan radiasi pita lebar. Mereka mencatat bahwa sifat optik es yang tidak konsisten dapat menyebabkan kesalahan sistematis ketika menghitung efek radiasi awan, dan kesalahan ini melebihi ketidakpastian observasional. Penulis menganjurkan pengembangan lebih lanjut dari model kristal es yang lebih konsisten secara mikrofisika dan optik seperti Baran, Cotton, et al . ( 2014a ) dan Liu et al . ( 2014 ) pendekatan model campuran dua-habit. Dalam studi sebelumnya oleh Bae et al . ( 2016 ), mereka menunjukkan peningkatan kesesuaian dengan irradiansi gelombang pendek yang diamati yang mencapai tanah dan pola presipitasi dengan secara konsisten menggabungkan skema mikrofisika Weather Research Forecasting (WRF) dua-momen enam-kelas (WDM6) dengan skema radiasi. Hal ini dicapai dengan menghitung secara dinamis dimensi karakteristik PSD untuk hidrometeor berdasarkan jumlah dan konsentrasi massanya. Karya Baran, Hill, et al . ( 2014b ), Bae et al . ( 2016 ), dan Ren et al.( 2023 ) menunjukkan pentingnya menghubungkan skema mikrofisika dan radiasi secara konsisten dalam model cuaca dan iklim untuk meningkatkan representasi proses radiasi.

Dimensi karakteristik PSD dalam skema radiasi umumnya didefinisikan dalam hal dimensi efektif, De , yang merupakan ukuran partikel rata-rata yang dibobot oleh area proyeksi kristal es yang berorientasi acak atau rasio antara kadar air es (IWC) dan koefisien kepunahan volume (Foot, 1988 ; Francis, 1995 ; McFarquhar & Heymsfield, 1998 ; Mitchell, 2002 ). Namun, penelitian oleh Francis ( 1995 ), Baran ( 2012 ), Baran, Hill, et al . ( 2014b ), Baran et al . ( 2016 ), dan Sieron et al . ( 2017 ) telah menunjukkan kekurangan dalam menggunakan metode berbasis dimensi yang efektif untuk menggambarkan sifat hamburan tunggal kristal es. Khususnya, kristal es, yang sifatnya kira-kira fraktal saat mereka beragregasi, akan memiliki dimensi massa dan area yang cenderung ke dimensi fraktal hampir dua atau kurang dari dua, masing-masing (Field et al ., 2008 ; Westbrook et al ., 2004 ). Karena De adalah rasio antara massa dan area, ia menjadi jauh lebih tidak berdampak radiatif saat kristal es beragregasi dengan jarak dari puncak awan. Atas alasan ini, Baran, Hill, et al . ( 2014b ) dan Baran et al . ( 2016 ) mengembangkan parameterisasi mikrofisika cirrus–radiasi yang konsisten yang menghubungkan sifat optik es curah secara langsung ke IWC dan suhu dalam awan. Parameterisasi ini mempertahankan konsistensi antara skema mikrofisika cirrus dan radiasi melalui IWC dan PSD, yang mana yang terakhir didasarkan pada Field et al . ( 2007 ) parameterisasi estimasi momen PSD, dihasilkan melalui hubungan massa-dimensi yang diturunkan oleh Cotton et al . ( 2013 ) dan suhu dalam awan.

Menariknya, Zhou et al . ( 2024 ) mengeksplorasi karakteristik data reflektansi tampak Fengyun-4A Advanced Geostationary Radiation Imager dan mengevaluasi ketidakpastian akibat kesalahan model. Fokus penting dari studi ini mencakup analisis sensitivitas radiansi yang disimulasikan dengan parameterisasi sifat optik awan es berdasarkan yang disediakan oleh Baran, Cotton, et al . ( 2014a ), selanjutnya disebut Baran, dan Baum et al . ( 2011 ), selanjutnya disebut Baum. Studi ini menunjukkan perbedaan sistematis antara dua parameterisasi ketika digunakan untuk mensimulasikan reflektansi tampak awan es, dengan parameterisasi Baran umumnya memberikan nilai reflektansi yang lebih tinggi daripada pendekatan Baum. Ini menunjukkan bahwa perbedaan parameterisasi ini merupakan kontributor utama ketidakpastian dalam sifat radiatif awan es. Namun, penulis mencatat keuntungan dalam pendekatan Baran karena hubungan langsungnya dengan variabel mikrofisika daripada bergantung pada parameterisasi yang melibatkan radius efektif, r e (yaitu, r e  =  D e /2). Mereka menemukan bahwa ketika model tidak secara langsung memprediksi r e dari skema mikrofisika awan, maka harus diperkirakan, yang dapat memperburuk kesalahan model maju ketika menggunakan parameterisasi Baum. Hal ini merupakan keterbatasan potensial parameterisasi sifat optik es yang dikaitkan dengan r e , yang dapat memengaruhi kegunaannya dalam perbandingan model transfer radiatif.

Dalam studi sebelumnya, Geiss et al . ( 2021 ) mengevaluasi representasi awan dalam model prediksi cuaca numerik (NWP) menggunakan pengamatan tampak dan inframerah dan kembali memeriksa perbedaan antara representasi sifat optik es Baran dan Baum. Mereka menemukan bahwa parameterisasi optik es curah Baran memberikan representasi yang konsisten dari reflektansi tampak untuk awan es yang tipis dan tebal secara optik. Namun, parameterisasi Baum meremehkan reflektansi tampak, terutama untuk awan es yang tipis secara optik, konsisten dengan temuan Zhou et al . ( 2024 ). Studi ini menyoroti keuntungan dari menghubungkan sifat optik es curah secara langsung ke IWC curah dan suhu, karena hubungan ini memberikan kerangka kerja yang lebih fleksibel, terutama jika tidak ada informasi mikrofisika yang terperinci. Namun, kesalahan model maju didominasi oleh perbedaan dalam representasi bentuk partikel es skema, asumsi hamburan, dan sensitivitas terhadap proses skala subgrid. Studi ini menemukan bahwa proses skala subgrid awan merupakan sumber kesalahan sistematis yang signifikan, terutama untuk reflektansi. Untuk meminimalkan kesalahan tersebut, penulis menyarankan untuk menjauh dari PSD momen tunggal. Mereka mengusulkan bahwa PSD dua momen atau bahkan PSD orde lebih tinggi dapat menangkap variabilitas alami dalam ukuran dan konsentrasi kristal es dengan lebih baik, yang berpotensi mengurangi bias dalam simulasi sifat radiasi awan.

Perbandingan menyeluruh dari sifat hamburan tunggal antara berbagai parameterisasi optik es (seperti Baran dan Baum) akan berharga untuk mengukur seberapa besar perbedaan sistematis dalam sifat radiasi yang disimulasikan berasal dari model partikel optik itu sendiri dibandingkan dengan penggunaan berbagai variabel penghubung (misalnya, radius efektif vs kuantitas mikrofisika langsung). Analisis semacam itu dapat membantu mengisolasi dampak spesifik dari asumsi kebiasaan, penanganan kekasaran permukaan, dan faktor mikrofisika lainnya pada prediksi perpindahan radiasi.

Jelas, parameterisasi optik es Baran, yang menghubungkan sifat optik es curah, IWC, dan suhu dalam awan, didasarkan pada satu momen. Dalam pembahasan sebelumnya, kami menyoroti keuntungan mengembangkan parameterisasi sifat optik es curah menggunakan mikrofisika dua momen untuk mengurangi ketidakpastian model maju. Selain itu, parameterisasi momen tunggal menghalangi kemungkinan terjadinya efek Twomey (Twomey, 1977 ). Ini karena parameterisasi momen tunggal, yang hanya memprediksi satu momen distribusi ukuran hidrometeor (biasanya rasio pencampuran massa), tidak memperhitungkan perubahan dalam jumlah konsentrasi tetesan awan. Keterbatasan ini menghalangi representasi akurat dari efek Twomey. Sementara penelitian sebelumnya, seperti Bae et al . ( 2016 ), secara dinamis menghubungkan jari-jari efektif ke skema radiasi menggunakan mikrofisika dua momen, pendekatan ini bergantung pada asumsi tentang jari-jari efektif yang dapat menimbulkan ketidakkonsistenan, seperti yang dicatat dalam pembahasan sebelumnya. Studi ini mengatasi keterbatasan ini dengan menggabungkan mikrofisika dua momen secara langsung dengan sifat optik es curah, yang memungkinkan simulasi medan radiasi yang lebih konsisten secara fisik. Hal ini dicapai dengan mengembangkan parameterisasi optik es curah cirrus baru berdasarkan dua momen (yaitu, rasio dan jumlah pencampuran massa es) untuk skema mikrofisika dua momen milik Met Office.

Bahasa Indonesia: Untuk meningkatkan representasi interaksi beberapa momen dalam GCM, sangat penting untuk memodelkan interaksi ini secara akurat pada tingkat fundamental untuk mereplikasi proses awan skala subgrid dengan lebih baik. Untuk mengatasi kebutuhan ini, Shipway dan Hill ( 2012 ), Hill et al . ( 2015 ), dan Field et al . ( 2023 ) mengembangkan Model Interaksi Awan dan Aerosol (CASIM) milik Met Office untuk menggabungkan efek beberapa momen dalam pemrosesan partikulat atmosfer di dalam awan. CASIM dirancang untuk menggantikan skema mikrofisika terkini yang digunakan dalam Model Terpadu dan model awan Met Office-NERC (MONC) untuk penggunaan jangka panjang (lihat Hill et al ., 2018 untuk detail tentang MONC). CASIM memungkinkan penggunaan beberapa spesies, termasuk jumlah konsentrasi air awan, hujan, es awan, salju, dan graupel. Es awan dan air awan dapat direpresentasikan oleh satu atau dua momen prognostik, sementara hujan, salju, dan graupel dapat menggunakan momen prognostik ketiga. Momen-momen prognostik ini mencakup konsentrasi jumlah, massa, dan beberapa representasi bentuk distribusi ukuran, seperti reflektivitas radar.

Dalam CASIM di Met Office, jumlah es dimulai melalui pembekuan homogen tetesan air dan nukleasi es heterogen. Ketika jumlah es tidak dimulai oleh aerosol, itu didasarkan pada hubungan Cooper ( 1986 ) antara jumlah es dan suhu awan, yang berfungsi sebagai latar belakang klimatologis. Dalam studi ini, kami menggunakan metode terakhir ini untuk produksi jumlah es di seluruh makalah. Pembentukan kristal es juga bergantung pada jumlah uap air yang ada dan suhu. Prediksi CASIM telah divalidasi melalui beberapa studi observasional, termasuk yang dilakukan oleh Leon et al . ( 2016 ), Miltenberger et al . ( 2018 ), dan Gordon et al . ( 2020 ) , yang menggunakan pesawat BAe-146 Facility for Airborne Atmospheric Measurements (FAAM), meskipun studi-studi ini terutama berfokus pada awan air dan hujan. ( 2018 ) menunjukkan bahwa mikrofisika dua momen CASIM secara konsisten mengungguli skema momen tunggal dalam mereproduksi sifat radiatif dan presipitasi awan yang diamati. Selain itu, ia menyediakan distribusi reflektivitas radar yang lebih selaras dengan pengamatan radar pita-S berbasis darat. Dengan menggabungkan pengamatan ini dengan pengembangan CASIM, kita dapat mengurangi ketidakpastian yang ada terkait dengan efek radiatif dari interaksi multimomen. Kuantitas yang tidak diketahui ini berkontribusi pada ketidakpastian yang besar dalam pemodelan dan estimasi observasional efek radiatif awan, seperti yang disorot dalam laporan IPCC, 2021 dan laporan sebelumnya.

Lebih efektif untuk menghubungkan variabel prognostik model, seperti massa dan jumlah konsentrasi, secara langsung ke sifat optik es daripada mengandalkan variabel perantara seperti radius efektif. Radius efektif bukanlah variabel prognostik dalam model cuaca dan iklim dan dapat menimbulkan kesalahan karena ketergantungannya pada asumsi tambahan. Pendekatan kami secara langsung menghubungkan simulasi perpindahan radiatif dalam CASIM ke pengamatan radiometrik, memfasilitasi evaluasi yang lebih baik terhadap pengamatan tersebut dan memungkinkan representasi efek radiatif yang lebih realistis, termasuk interaksi aerosol–es.

Makalah ini dibagi menjadi beberapa bagian. Bagian 2 memberikan tinjauan singkat tentang model ensemble kristal es cirrus (yaitu, model yang menjadi dasar parameterisasi optik es konsisten yang digabungkan) yang dikembangkan oleh Baran dan Labonnote ( 2007 ), bersama dengan definisi sifat optik es massal. Di Bagian 3 , kami menjelaskan PSD CASIM yang diasumsikan, bersama dengan momen yang diperlukan dan asumsi massa yang digunakan untuk menghasilkan PSD. Bagian 4 merinci data CASIM yang digunakan untuk menghasilkan PSD dari mikrofisika dua momen prognostik untuk mengembangkan parameterisasi optik es. Di Bagian 5 , kami menjelaskan parameterisasi baru yang sepenuhnya konsisten. Bagian 6 menyajikan studi kasus regional Darwin, Australia, yang digunakan untuk mengevaluasi kinerja parameterisasi optik es baru terhadap pengukuran iradiasi gelombang pendek dan gelombang panjang CERES. Hasil dari seluruh Inggris juga disajikan di bagian ini. Akhirnya, Bagian 7 membahas kesimpulan yang diambil dari makalah ini.

2 MODEL ENSEMBLE KRISTAL ES CIRRUS
Model ensemble kristal es cirrus dikembangkan oleh Baran dan Labonnote ( 2007 ) dan direproduksi di sini sebagai Gambar 1. Gambar tersebut menunjukkan bahwa model ensemble terdiri dari enam elemen, yang pertama adalah kolom es heksagonal dengan rasio aspek kesatuan, dan elemen kedua adalah roset peluru bercabang enam. Setelah itu, monomer heksagonal secara sembarangan melekat satu sama lain sebagai fungsi dimensi maksimum, D max , membentuk agregat es heksagonal tiga hingga sepuluh elemen. Elemen-elemen tersebut dibangun agar tidak mengandung bidang yang berpotongan, dan monomer melekat sedemikian rupa sehingga beberapa refleksi antara monomer dapat diabaikan, yang ditentukan secara eksperimental menggunakan kalkulasi ray-tracing. Elemen pertama mewakili ukuran kristal es yang lebih kecil di PSD, sedangkan agregat es heksagonal mewakili proses agregasi kristal es dan, dengan demikian, kristal es berukuran lebih besar di PSD. Dalam makalah ini, setiap partikel dari model ensemble ditempatkan dalam wadah ukuran PSD sesuai urutan dan tidak diberi bobot dalam wadah ukuran mana pun. Bentuk setiap anggota model ensemble ditunjukkan pada Gambar 1 .

Gambar 2 menunjukkan distribusi anggota model ansambel sebagai fungsi dimensi maksimum dalam setiap rentang ukuran yang ditunjukkan pada gambar, di mana distribusi setiap anggota seragam di setiap rentang ukuran.

Seperti yang digambarkan dalam Gambar 2 , agregasi kristal es meningkat seiring dengan peningkatan dimensi maksimum partikel. Proses peningkatan agregasi dengan ukuran partikel ini konsisten dengan pengamatan Field et al . ( 2008 ) dan Lawson et al . ( 2019 ), serta referensi yang dikutip di dalamnya. Saat agregasi kristal es meningkat, rasio area (yaitu, rasio area proyeksi rata-rata orientasi partikel non-bulat ke area proyeksi bola yang dibatasi yang memiliki dimensi maksimum yang sama dengan partikel non-bulat) dari agregat cenderung ke arah nilai sekitar 0,5 atau kurang, menurut Field et al . ( 2008 ). Rasio area model ensemble mengikuti tren yang sama dengan pengamatan saat dimensi maksimum meningkat, dan mereka jatuh dalam ketidakpastian pengamatan mikrofisika, seperti yang ditunjukkan dalam Baran et al . ( 2015 ).

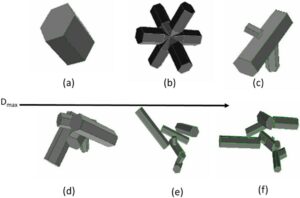
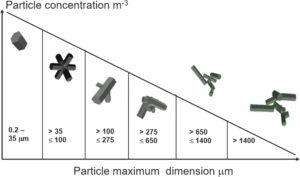
Pilihan kebiasaan yang disajikan dalam Gambar 1 mengikuti literatur yang diterbitkan tentang agregasi dan morfologi kristal es yang ditemukan di cirrus pada saat itu. Alasan utama diterbitkan dalam Baran dan Labonnote ( 2007 , Bagian 3, hlm. 1902), yang tidak kami ulangi di sini karena alasan singkatnya. Namun, kolom es heksagonal yang ditunjukkan dalam Gambar 1a dan 2 dipilih untuk mewakili kristal es yang lebih kecil (<35 μm) berdasarkan bukti in-situ dari Korolev dan Isaac ( 2003 ), yang menunjukkan bahwa partikel berukuran kurang dari 30–40 μm biasanya menunjukkan rasio aspek yang mendekati kesatuan, dan kristal es kecil ini tidak berbentuk bulat di alam. Model ensemble berfokus pada bentuk kolom dan agregatnya daripada kristal seperti pelat karena, seperti yang ditunjukkan, setelah Baran dan Labonnote ( 2007 ), oleh Bailey dan Hallett ( 2009 ), agregat kolom mendominasi pada suhu di bawah sekitar −40°C, yang merupakan kondisi khas pembentukan kristal es murni di cirrus. Studi oleh Bailey dan Hallett ( 2009 ) telah memberikan dukungan observasional lebih lanjut untuk dominasi agregat kolom pada suhu pembentukan cirrus.

Properti hamburan massal yang diprediksi oleh distribusi anggota model ensemble yang ditunjukkan pada Gambar 2 telah dievaluasi terhadap pengamatan aktif dan radiometrik dari berbagai kampanye pesawat terbang dan pengamatan satelit multispektral. Prediksi model ensemble berada dalam ketidakpastian pengukuran aktif dan radiometrik dalam studi yang dilakukan oleh Baran, Cotton, et al . ( 2014a ) dan Sourdeval et al . ( 2015 , 2016 ). Baru-baru ini, Röttenbacher et al . ( 2024 ) memberikan evaluasi terperinci dari beberapa parameterisasi optik es, yaitu Fu-IFS (Fu, 1996 ), Yi et al . ( 2013 ), dan Baran et al . ( 2016 ), dalam skema radiasi ecRad dari Pusat Prakiraan Cuaca Jangka Menengah Eropa (ECMWF; Hogan & Bozzo, 2018 ) untuk simulasi transmisivitas matahari dari sirus Arktik. Sementara perbandingan awal menggunakan IWC yang diprediksi model dan radius efektif hanya menunjukkan sedikit perbedaan di antara ketiga parameterisasi, uji sensitivitas menggunakan IWC yang diambil menunjukkan perbedaan yang lebih nyata. Secara khusus, untuk cirrus Arktik yang tebal secara optik, Fu-IFS dan Yi2013 melebih-lebihkan transmisivitas surya, sedangkan Baran2016 memberikan kesesuaian yang sedikit lebih baik dengan pengukuran. Röttenbacher et al . ( 2024 ) juga menyoroti bahwa parametrisasi Baran2016, berdasarkan pengukuran kristal es in-situ terkini dan menggunakan parametrisasi estimasi momen PSD oleh Field et al . ( 2007 ), menawarkan ketahanan statistik yang lebih baik di seluruh rentang IWC dan kondisi suhu yang khas di Arktik. Selain itu, Baran2016 menghilangkan ketergantungan pada asumsi radius efektif, yang dianggap sebagai keuntungan relatif terhadap skema Fu-IFS dan Yi2013.

2.1 Perhitungan sifat optik massal
SOCRATES (Suite Of Community RAdiative Transfer codes based on Edwards and Slingo) adalah skema radiasi yang digunakan dalam pekerjaan sains Bumi dan planet milik Met Office dan dijelaskan oleh Manners et al . ( 2023 ). Properti hamburan tunggal yang digunakan dalam studi ini dihitung dengan asumsi kristal es berorientasi acak dalam ruang 3D. Dengan demikian, perhitungan tidak secara eksplisit menyertakan efek yang disebabkan oleh orientasi jatuh yang istimewa. Di sini, untuk mensimulasikan medan radiasi, SOCRATES menggunakan masukan dari CASIM untuk memecahkan iradiasi keluar melalui perkiraan dua aliran dalam model transfer radiatif Edwards–Slingo (Edwards & Slingo, 1996 ). Untuk tujuan ini, hanya properti optik massal yang diperlukan, karena perkiraan transfer radiatif dua aliran digunakan untuk menghitung medan radiasi keluar; ini adalah koefisien kepunahan massal ( C ext ), hamburan ( C sca ) dan penyerapan ( C abs ), serta albedo hamburan tunggal ( ω 0 ) dan parameter asimetri ( g ). Definisi dari sifat optik massal ini adalah sebagai berikut:

Pada Persamaan ( 4 ), semua istilah telah didefinisikan sebelumnya. Persamaan ( 1-4 )–( 1-4 ) digunakan untuk menghitung sifat optik massal model ensemble pada 170 panjang gelombang antara panjang gelombang 0,175 dan 100 μm.
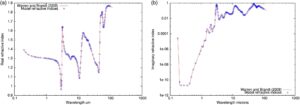
Resolusi panjang gelombang yang digunakan untuk menghitung sifat optik massal model ensemble ditunjukkan pada Gambar 3a,b . Gambar-gambar tersebut menunjukkan indeks es padat yang nyata dan imajiner, sebagaimana disusun oleh Warren dan Brandt ( 2008 ), dengan lingkaran terbuka yang ditumpangkan pada indeks bias yang mewakili panjang gelombang di mana sifat optik massal dihitung. Dari gambar-gambar tersebut, jelas bahwa resolusi panjang gelombang yang digunakan dalam makalah ini memadai untuk menangkap variasi cepat dalam indeks bias es, khususnya antara 1,5 μm dan 4,0 μm, dan pada panjang gelombang di jendela terestrial dan wilayah inframerah jauh.

Perhitungan sifat hamburan tunggal dari masing-masing anggota model ensemble antara panjang gelombang 0,175 dan 100 μm sekarang dijelaskan dan mengikuti deskripsi dalam Baran, Cotton, et al . Pada panjang gelombang antara 0,2 dan 4,9 μm, sifat optik total (yaitu, sifat optik integral, yang diberikan oleh Persamaan 1-4 ) dihitung menggunakan metode penelusuran sinar Monte Carlo yang dikembangkan oleh Macke et al . ( 1996 ); setiap elemen ensemble diacak menggunakan metode distorsi, dan pengacakan maksimum dicapai menggunakan distorsi dan menyertakan kristal es dengan gelembung udara bulat. Metode distorsi dijelaskan dalam Macke et al . ( 1996 ); namun, deskripsi singkat tentang metode diberikan di sini. Untuk setiap peristiwa refleksi dan refraksi di antarmuka faset cembung, sudut kemiringan, θ t , divariasikan secara acak sementara fungsi kerapatan probabilitas seragam diasumsikan. Ini mengubah arah lintasan sinar, yang memiliki efek menghilangkan energi dari daerah halo dan busur es dan mendistribusikannya kembali ke sudut hamburan samping yang lebih banyak (yaitu, sudut di mana sinar dibelokkan), menghasilkan nilai parameter asimetri yang lebih rendah, relatif terhadap padanannya yang murni. Distorsi adalah metode geometri skala besar yang seharusnya merepresentasikan kekasaran permukaan skala mikro dan ketidakteraturan kristal es. Derajat distorsi didefinisikan sebagai θ t  / 90° dan dapat mengambil nilai antara 0 (murni) dan 1. Dalam makalah ini, seperti yang dijelaskan dalam Baran dan Labonnote ( 2007 ), kami menerapkan nilai distorsi 0,4 ditambah inklusi gelembung udara bulat ke semua enam elemen model ansambel. Inklusi gelembung udara bulat diatur ke panjang lintasan bebas rata-rata 200 μm di seluruh model. Nilai distorsi sebesar 0,4 dipilih karena nilai ini ditemukan paling sesuai dengan pengukuran POLDER-2 (POLarization and Directionality of the Earth’s Reflectances, lihat Buriez et al ., 2005 ) dari albedo sferis dan reflektansi terpolarisasi linier (Baran & Labonnote, 2006 ). Untuk nilai distorsi sebesar 0,4 ditambah inklusi gelembung udara sferis, modifikasi yang dibuat pada kode penelusuran sinar Macke et al . ( 1996 ) oleh Shcherbakov et al . ( 2006 ) telah digunakan. Karena angka acak yang mewakili θ t ditemukan oleh Shcherbakov et al . ( 2006)) agar dapat direpresentasikan dengan lebih baik oleh statistik Weibull ketimbang fungsi kerapatan probabilitas seragam, statistik Weibull lebih sesuai dengan pengukuran hamburan sudut tampak ruang awan dari fungsi fase.

Pada panjang gelombang lebih besar dari 5,0 μm, total sifat optik dihitung menggunakan metode Baran ( 2003 ). Dalam metode ini, total sifat optik dihitung menggunakan metode T-matrix (Mishchenko & Travis, 1998 ) dengan menerapkan perkiraan hamburan elektromagnetik agregat yang dikembangkan oleh Baran ( 2003 ). Baran ( 2003 ) menunjukkan bahwa pada panjang gelombang di wilayah jendela terestrial, perhitungan domain waktu beda hingga dari total sifat optik agregat es heksagonal (Yang & Liou, 1998 ) dapat dihitung hingga 4% dari solusi eksak menggunakan perkiraan tersebut. Tingkat akurasi ini dicapai dengan memperkirakan agregat menggunakan ansambel silinder melingkar dengan rasio volume-ke-luas yang sama dengan rasio aspek yang bervariasi. Aproksimasi elektromagnetik dan model es yang sama digunakan oleh Baran dan Francis ( 2004 ) untuk mensimulasikan pengukuran ARIES dalam ±1 K, antara panjang gelombang 3,4 dan 16,0 μm, yang diperoleh di atas cirrus semi-transparan di lepas pantai timur laut Skotlandia selama Oktober 2000.

Pada bagian berikutnya, PSD CASIM akan didefinisikan dan dijelaskan. PSD ini akan digunakan untuk mengintegrasikan sifat hamburan tunggal guna menentukan sifat optik massal menggunakan Persamaan ( 1-4 )–( 1-4 ).

3 PSDS CASIM
PSD CASIM direpresentasikan oleh distribusi gamma umum (Field et al ., 2023 ), dan bentuk PSD yang sama ini digunakan untuk menghasilkan sifat optik es curah model ensemble. Bentuk distribusi gamma umum dijelaskan oleh persamaan berikut:

di mana subskrip i dan s telah dihilangkan dari semua istilah untuk memudahkan pembacaan. Istilah m 1 dan m 2 masing-masing adalah momen massa dan momen angka; m 1 terkait dengan massa melalui hubungan massa–dimensi, m 1  = massa/ C x , di mana C x adalah kerapatan es dan salju. Satuan massa dalam kg per kg udara berawan per satuan volume, dan satuan angka dalam per kg udara berawan per satuan volume. Istilah P 1 dan P 2 dalam Persamaan ( 6 ) mewakili eksponen persamaan momen, M ( P ), dari PSD untuk massa dan angka, masing-masing. Persamaan momen diberikan oleh M ( P ) = ∫ N ( D ) D P dD .
Partikel es dalam CASIM diasumsikan spasial, mewakili roset peluru dan polikristal; jadi, P 1  = 3,0, C x  = 104,7 kg m −3 , dan P 2  = 0 dengan μ  = 2,5. Dalam kasus es, dengan P 1  = 3,0, pengaturan ini mengasumsikan bahwa massa es proporsional dengan momen ketiga PSD. Untuk salju, P 1  = 2,0 dan C x  = 0,026 kg·m −3 , konsisten dengan hubungan massa–dimensi yang diusulkan oleh Cotton et al . ( 2013 ) yang merepresentasikan massa partikel es yang beragregasi. Hubungan ini saat ini digunakan dalam skema mikrofisika es Model Sistem Bumi milik Met Office. Hubungan massa–dimensi ini selaras dengan hukum pangkat massa–dimensi yang diturunkan secara independen lainnya yang ditemukan dalam literatur. Misalnya, Cotton et al . ( 2013 ) menunjukkan kesesuaian yang kuat dengan hukum pangkat yang diperoleh oleh Heymsfield et al . ( 2010 ). Selain itu, Erfani dan Mitchell ( 2016 ) menemukan konsistensi serupa dalam analisis mereka. Baru-baru ini, McCusker et al . ( 2024 ) menunjukkan bahwa hukum pangkat Cotton et al . ( 2013 ) juga sesuai dengan hubungan Brown dan Francis ( 1995 ), asalkan perbedaan dalam definisi ukuran diperhitungkan, dengan mengikuti Hogan et al . ( 2012 ). Untuk salju, P 2  = 0, tetapi μ  = 2,0. Perlu dicatat di sini bahwa prefaktor yang diasumsikan sebesar 104,7 kg·m −3 untuk es memberikan kerapatan efektif sekitar 200 kg·m −3 , yang berbeda dengan nilai turunan in-situ sebesar 700 kg·m −3 yang ditemukan oleh Cotton et al . ( 2013 ). Namun, Heymsfield dkk . ( 2004 ) menemukan kepadatan in-situ berkisar antara sekitar 100 hingga sekitar 400 kg·m −3 dalam kasus yang mereka ambil sampelnya. Oleh karena itu, masih terdapat keleluasaan yang cukup besar dalam pemilihan nilai kepadatan efektif untuk es.

Untuk mendapatkan jumlah konsentrasi total, N T ( D ), di setiap bin ukuran lebar dD , dua PSD unimodal yang direpresentasikan oleh Persamaan ( 5 ) ditambahkan bersama-sama sebagai berikut:

Untuk mematuhi dimensi Persamaan ( 5 ), satuan massa salju dan es, dan jumlah dari keluaran CASIM diubah menjadi satuan kg m −3 dan m −3 , masing-masing, melalui kerapatan udara kering (kg m −3 ), yang diperoleh dari keluaran CASIM. Pada suhu pembentuk cirrus, perbedaan antara kerapatan udara kering dan udara lembap dapat diabaikan. Oleh karena itu, pilihan kerapatan udara dalam makalah ini tidak penting. Dalam makalah ini, rentang ukuran yang dipertimbangkan bervariasi dari 1 hingga 28.121 μm, dan lebar bin untuk setiap PSD ditetapkan pada 10 μm.
Kami membandingkan PSD turunan CASIM dengan PSD yang diasumsikan dalam parametrisasi optik es terkini dalam Model Sistem Bumi milik Met Office (lihat Walters et al ., 2019 ) berdasarkan Baran et al . ( 2016 ), yang diperoleh dari parametrisasi estimasi momen oleh Field et al . ( 2007 ). Ini menggunakan normalisasi tropis PSD dari Field et al . ( 2007 ) karena bentuk PSD ini sesuai dengan pengamatan momen dan PSD in-situ, seperti yang ditunjukkan oleh Furtado et al . ( 2015 ) dan Baran et al . ( 2011 ), masing-masing. Untuk menghasilkan PSD Field et al . ( 2007 ), juga dikenal sebagai F07, total IWC dan suhu lingkungan diperlukan sebagai input untuk parametrisasi, serta hubungan massa-dimensi yang diasumsikan, yaitu Cotton et al . ( 2013 ) hubungan.

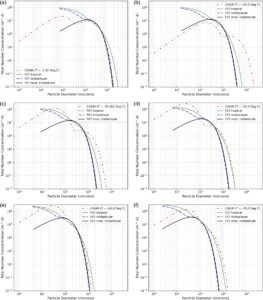
Gambar 4 menunjukkan contoh PSD yang diprediksi oleh CASIM untuk berbagai total IWC dalam awan (yaitu, jumlah IWC es dan salju), dan nilai N T dalam awan , pada enam suhu lingkungan. Untuk memperoleh suhu lingkungan, T k , dari data model, kami menggunakan suhu dalam Kelvin pada tingkat model.

Gambar 4 bertujuan untuk mengilustrasikan rentang dalam PSD CASIM untuk dua masukan momen yang diberikan. Selain itu, gambar tersebut menampilkan PSD F07 tropis, lintang tengah, dan lintang tengah yang dimodifikasi yang ekuivalen. PSD F07 lintang tengah yang dinormalisasi asli baru-baru ini telah diperbarui untuk memperhitungkan pengamatan terkini dari konsentrasi jumlah kristal es kecil dengan ukuran di bawah 100 μm; rujuk O’Shea et al . ( 2021 ) untuk detail lebih lanjut. Namun, deskripsi singkat dari PSD F07 lintang tengah yang dimodifikasi diberikan di sini. PSD lintang tengah F07 dimodifikasi untuk memperhitungkan pengamatan terkini yang menunjukkan bahwa banyak kristal es kecil dapat berukuran salah dan karenanya secara tidak tepat berkontribusi pada konsentrasi jumlah serta artefak pecah yang potensial bahkan setelah penyaringan waktu antar kedatangan. Modifikasi tersebut menghapus mode partikel yang lebih kecil dari distribusi dan menerapkan faktor koreksi yang sesuai pada hubungan momen untuk menjaga konsistensi dalam distribusi keseluruhan. Hal ini menghasilkan partikel kecil yang lebih sedikit (<100 μm) dalam PSD yang dimodifikasi dibandingkan dengan parameterisasi lintang tengah F07 asli. Tabel 1 mencantumkan berbagai nilai total IWC dalam awan, N T dalam awan , dan T k yang digunakan untuk perbandingan Gambar 4 , di mana dalam gambar T k telah diubah menjadi o C.

TABEL 1. Berbagai nilai T _c , nilai total IWC dalam awan, dan N _T yang dipilih secara acak digunakan untuk menghasilkan PSD CASIM dan F07 yang ditunjukkan pada Gambar  4.

Catatan : IWC, kandungan air es; PSD, distribusi ukuran partikel.

Pada Gambar 4 , CASIM PSD dapat sama lebarnya atau bahkan lebih lebar dari F07 PSD. Namun, bentuk CASIM PSD dapat bervariasi secara signifikan tergantung pada masukan dua momen, meskipun mode es dan salju hadir pada semua suhu yang dipertimbangkan. Perlu dicatat bahwa parametrisasi F07 PSD didasarkan pada pengukuran in-situ yang diperoleh pada suhu tidak lebih dingin dari sekitar −65°C. Tujuan Gambar 4 adalah untuk mengilustrasikan berbagai bentuk CASIM PSD dan bagaimana ini dibandingkan dengan F07 Tropical PSD yang digunakan dalam parametrisasi optik es saat ini yang digunakan dalam GCM. Perbandingan ini berguna dalam menjelaskan perbedaan yang diamati dalam simulasi radiasi antara parametrisasi CASIM baru dan parametrisasi optik es saat ini. Perlu dicatat bahwa tidak semua CASIM PSD akan seperti yang disajikan pada Gambar 4 , karena variasi dalam bentuk CASIM PSD dapat sangat signifikan tergantung pada masukan es dan salju. Bagian berikutnya membahas ekstraksi masukan dua momen dari pengujian model regional.

4 DATA DUA MOMEN CASIM
Data CASIM yang digunakan dalam studi ini diambil dari model regional yang dijalankan dipusatkan di Darwin, Australia, dan Inggris Raya. Data (dari model regional) yang digunakan untuk membangun parameterisasi sifat optik es curah diambil dari perkiraan yang dijalankan setelah satu hari untuk Darwin dan Inggris Raya untuk memungkinkan beberapa evolusi bidang berawan. Dalam kasus Darwin, data yang diekstraksi sesuai dengan tengah hari dan tengah malam setempat untuk periode antara 23 Januari dan 17 Maret 2017. Dalam kasus Inggris Raya, data diekstraksi dari tengah hari setempat selama periode antara 6 Desember 2017 dan 01 Maret 2018. Data diekstraksi dari periode musim panas dan musim dingin untuk mencakup rentang nilai momen es dan salju yang seluas-luasnya untuk konstruksi parameterisasi sifat optik es curah. Baik wilayah Inggris Raya maupun Darwin mencakup sekitar 1000 km 2 . Kasus Darwin mengandung konveksi tropis yang dalam dan kumulus yang hanya hangat. Wilayah Inggris Raya mengandung awan lintang tengah. Kedua domain tersebut memiliki wilayah daratan dan lautan. Area-area ini sama dengan yang digunakan dalam makalah Bush et al . ( 2024 ). Dari dua model regional, sebagian dari total data es dan salju diekstraksi.

Subset data ini diekstraksi untuk memastikan data yang digunakan dalam parameterisasi properti optik massal akan aktif secara radiatif, dan bahwa nilai dalam awan masuk akal saat dikonversi dari nilai rata-rata kotak gridnya. Untuk tujuan ini, fraksi awan yang diekstraksi tidak kurang dari 0,05, karena nilai yang lebih kecil dari ini kemungkinan tidak akan terdeteksi oleh pengamatan radiometrik berbasis ruang angkasa seperti yang disarankan dalam penelitian oleh Wang dan Zhao ( 2016 ). Di sini, tidak terdeteksinya fraksi awan yang kurang dari 0,05 oleh pengamatan radiometrik diambil sebagai proksi apakah awan tersebut aktif secara radiatif. Lebih lanjut, total IWC kurang dari 0,002 g·m −3 dikeluarkan dari subset data, dan jumlah konsentrasi total kurang dari 100 m −3 juga dikeluarkan dari analisis. Ini karena nilai IWC kurang dari ambang batas di atas akan memiliki jumlah terintegrasi kolom yang sangat kecil, dan awan ini tidak akan berinteraksi secara signifikan dengan medan radiasi. Ambang batas IWC total ditetapkan pada 0,002 g·m −3 karena ini adalah batas yang dapat dideteksi oleh probe IWC in-situ sebagaimana ditemukan dalam penelitian oleh Abel et al . ( 2014 ). Demikian pula, dalam kasus jumlah konsentrasi total, batas ambang batas 100 m −3 ditetapkan karena instrumen in-situ yang digunakan dalam penelitian global oleh Krämer et al . ( 2016 ) tidak menyertakan jumlah konsentrasi yang kurang dari ini.

Subset data yang diekstrak dari studi kasus Darwin dan Inggris menggunakan filter di atas meliputi tengah hari dan tengah malam setempat. Dari kumpulan data ini, distribusi terbaik nilai jumlah es dan salju dipilih, dan hari-hari ini digabungkan menjadi satu set data tunggal dari data Darwin dan Inggris. Distribusi jumlah dan massa es dan salju dari set data tunggal ini ditunjukkan pada Gambar 5a,b sebagai plot histogram bivariat. Batang yang ditunjukkan di sisi kanan Gambar 5a,b menunjukkan jumlah titik data dalam setiap bin, dengan skala berkisar dari kejadian tunggal hingga ribuan. Visualisasi ini dengan jelas mengungkapkan hubungan massa-angka yang paling umum dalam set data.

Pada Gambar 5a , distribusi kristal es yang luas terlihat dengan wilayah kepadatan tinggi yang menunjukkan korelasi positif antara jumlah es dan massa. Wilayah terpadat muncul pada nilai jumlah es dan massa sedang. Gambar 5b mengungkapkan pola yang jelas untuk partikel salju, dengan dua pita kepadatan tinggi yang menonjol yang menunjukkan hubungan massa-jumlah yang berbeda. Struktur diagonal ini kemungkinan mewakili proses pembentukan atau pertumbuhan salju yang berbeda yang terjadi dalam simulasi model. Titik-titik yang jarang penduduknya di sekitar pinggiran kedua distribusi menunjukkan kombinasi yang jarang dari nilai jumlah dan massa, yang secara efektif menyoroti batas-batas ruang parameter yang realistis secara fisik dalam model.

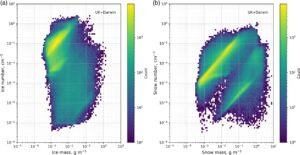
Distribusi data lengkap untuk setiap lokasi untuk semua hari tidak ditampilkan demi singkatnya. Dari Gambar 5 , momen es dan salju tampak sebagai distribusi yang cukup realistis untuk mendasarkan parameterisasi optik es dan terdistribusi dengan baik dalam ruang momen. Ini mungkin membantu menjelaskan mengapa PSD CASIM pada Gambar 4 lebih baik dibandingkan dengan PSD F07, yang terakhir diketahui mewakili PSD yang diamati.

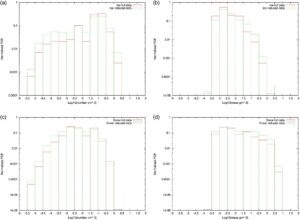
Gambar 5 menunjukkan jumlah total sekitar 10 8 titik data, yang terlalu besar untuk menghasilkan PSD dan menyimpan properti optik dalam SOCRATES. Untuk mengurangi jumlah titik ini ke ukuran yang lebih mudah dikelola, pengambilan sampel acak dilakukan untuk mendapatkan kumpulan data yang diperkecil, menghasilkan 62.250 PSD CASIM. Untuk menunjukkan bahwa tidak ada bias yang dimasukkan ke dalam kumpulan data yang diperkecil, Gambar 6 menyajikan perbandingan distribusi frekuensi konsentrasi jumlah es dan kandungan air es dalam kumpulan data yang tidak diperkecil dan yang diperkecil. Jelas dari Gambar 6 bahwa tidak ada perbedaan statistik antara fungsi kerapatan probabilitas (PDF) dari kumpulan data dua momen yang tidak diperkecil dan yang diperkecil. Oleh karena itu, mengurangi kumpulan data asli secara acak ke ukuran yang memungkinkan perhitungan efisien properti optik es curah tidak akan menimbulkan bias apa pun dalam momen prognostik CASIM.

5 PARAMETRISASI SIFAT OPTIK ES MASSAL CASIM
Sifat optik massal dari model ensemble telah dihitung menggunakan distribusi anggota ensemble seperti yang dijelaskan dalam Bagian 2. Sifat optik massal telah dihitung menggunakan input CASIM (yaitu, massa es di dalam awan dan massa salju di dalam awan, dan jumlah es di dalam awan dan jumlah salju di dalam awan) yang dijelaskan dalam Bagian 3 dan 4 untuk memperoleh PSD fungsi gamma umum yang diprediksi CASIM yang disajikan dalam Bagian 3. Ini tidak memiliki ketergantungan pada suhu di dalam awan, dan hanya massa total di dalam awan dan jumlah total, yang diprediksi oleh CASIM dan mereka dalam satuan kg·kg −1 dan jumlah·kg −1 masing-masing, dan terkait dengan sifat optik es massal. Ini menghilangkan kebutuhan untuk konversi satuan dalam model. 62.250 CASIM PSD digunakan untuk menghitung sifat optik es massal menurut Persamaan ( 1-4 )–( 1-4 ), yaitu koefisien kepunahan massal dan hamburan, C ext , dan C sca , masing-masing, albedo hamburan tunggal, ω 0 , dan parameter asimetri, g .

Di sini, telah dibuat basis data yang terdiri dari 62.250 nilai rasio pencampuran massa es di dalam awan dan jumlah totalnya. Nilai-nilai ini diikuti oleh 170 panjang gelombang antara 0,175 dan 100 μm, dan pada setiap panjang gelombang, koefisien hamburan dan penyerapan massal serta parameter asimetri disediakan. Namun, total ukuran basis data adalah 667 MB; ini adalah ukuran yang terlalu besar untuk diimplementasikan dalam berkas spektral SOCRATES, sehingga harus dikurangi ke ukuran yang lebih mudah dikelola. Untuk mencapai ini, rutinitas baru dalam SOCRATES yang disebut reduce_casim_ice disediakan, yang berulang kali membagi dua data menjadi beberapa bagian yang berisi jumlah titik data yang sama dalam urutan rasio pencampuran massa dan massa partikel rata-rata (yaitu, rasio antara total massa es di dalam awan dan jumlah total di dalam awan). Kemudian mengeluarkan basis data yang diperkecil sebanyak 1026 blok properti yang dirata-ratakan untuk mengurangi ukuran basis data hingga menjadi 14 MB dalam format yang dapat dibaca oleh rutin scatter_average yang ada dalam SOCRATES.

Teknik perataan spektral yang digunakan dalam makalah ini didasarkan pada studi Hogan dan Matricardi ( 2022 ), yang menemukan bahwa, mengikuti Edwards dan Slingo ( 1996 ), menggunakan perataan spektral ‘tipis’ dan ‘tebal’ lebih akurat dalam mereplikasi iradiasi awan daripada menggunakan teknik lain. Untuk awan tipis optik atau cirrus dengan kedalaman optik rendah, perataan linier sesuai untuk menghitung sifat optik. Dalam kasus ini, koefisien kepunahan massa, ko-albedo, dan parameter asimetri dirata-ratakan secara spektral (dibobot dengan iradiasi matahari atau Planck) seperti yang telah dilakukan sebelumnya. Ini disebut perataan ‘tipis’ karena pembobotan linier seperti itu dari sifat optik hanya tepat dalam batas awan tipis optik. Namun, dalam model dan pengamatan, sebagian besar awan tidak tipis optik. Dalam kasus ini, lebih tepat untuk menggunakan pembobotan yang lebih baik untuk sifat radiatif awan tebal optik. Untuk awan tebal secara optik atau rata-rata spektral ‘tebal’, koefisien refleksi awan tebal secara optik tak terhingga dihitung, dan dibobot, dan total kepunahan dibobot daripada koefisien individual. Hogan dan Matricardi ( 2022 ) menyimpulkan bahwa rata-rata spektral ‘tebal’ adalah pilihan terbaik untuk sebagian besar kasus penghitungan iradiasi awan. Dalam makalah sebelumnya, rekomendasi Edwards dan Slingo ( 1996 ) diikuti, yaitu bahwa rata-rata spektral ‘tipis’ dan ‘tebal’ harus diterapkan pada awan sirus dan air, masing-masing. Di sini, kami menguji rata-rata spektral ‘tebal’ dan ‘tipis’.

Kecocokan yang diperoleh menggunakan aproksiman Padé dengan berkas spektral gelombang pendek enam-pita standar dan gelombang panjang sembilan-pita ditemukan sangat baik untuk semua rentang panjang gelombang untuk berkas spektral ini. Pita yang digunakan, seperti yang disajikan oleh Walters et al . ( 2019 ), disediakan dalam Tabel 2 dan 3. Contoh kecocokan aproksiman Padé untuk pita spektral 3 disajikan dalam Gambar 7. Semua pita lainnya dipasang dengan sama baiknya, dan semua pita dapat ditemukan dalam Informasi Pendukung, yang disajikan dalam Gambar S1 –S5. Perlu dicatat bahwa dalam Gambar S1 , kecocokan dengan ko-albedo untuk pita 1 dan 2 tampak buruk. Ini karena ko-albedo untuk kedua pita ini sangat dekat dengan nol, yang secara efektif menunjukkan tidak ada penyerapan. Dalam memperoleh Gambar 7 , sifat optik es curah, rasio pencampuran massa es dalam awan, dan konsentrasi jumlah es awalnya dihitung menggunakan 62.250 PSD berbeda yang berasal dari CASIM. Untuk membuat analisis selanjutnya dapat dihitung secara komputasi, kumpulan data yang luas ini dikurangi dengan mengelompokkan PSD ke dalam 1026 tempat sampah. Yang penting, tempat sampah ini tidak dibentuk hanya dengan merata-ratakan sifat dalam interval yang sama dari massa partikel rata-rata. Sebaliknya, tempat sampah tersebut dihasilkan dengan membagi dua seluruh kumpulan data berulang kali menjadi jumlah PSD yang sama dalam ruang parameter dua dimensi, yang ditentukan oleh rasio pencampuran massa dan massa partikel rata-rata per partikel.

TABEL 2. Pita spektral untuk pita gelombang pendek. Tabel ini diadaptasi dari Walters et al.  ( 2019 )

Pendekatan yang disengaja ini dipilih secara eksplisit untuk mempertahankan potensi ketergantungan sifat optik pada kedua parameter mikrofisika ini. Namun, setelah diperiksa, menjadi jelas bahwa sifat optik massal menunjukkan sensitivitas minimal terhadap variasi rasio pencampuran massa. Akibatnya, titik data dari wadah tak beraturan ini sebagian besar runtuh ke fungsi monotonik massa partikel rata-rata per kristal es. Fitur ini membenarkan penggunaan massa kristal es rata-rata – dan khususnya jari-jari bola setara massa – sebagai variabel utama untuk menyesuaikan perkiraan Padé.

Dengan demikian, meskipun hubungan antara radius bola ekivalen massa dan sifat optik massal tampak terdefinisi dengan jelas pada Gambar 7 karena pengelompokan, strategi pengelompokan awal itu sendiri tidak secara inheren memaksakan hubungan ini. Sebaliknya, hal itu muncul secara alami dari data. Hal ini selanjutnya ditunjukkan dalam Informasi Pendukung (Gambar S6–S8 ), yang menunjukkan koefisien kepunahan massa berskala, koefisien hamburan massa, dan parameter asimetri yang diturunkan dari semua 62.250 PSD untuk Band 3 dari pita Edwards–Slingo gelombang panjang. Pendekatan penskalaan yang sama yang dijelaskan dalam keterangan Gambar 7 telah diterapkan. Gambar tambahan ini mengonfirmasi bahwa sifat optik massal runtuh ke kurva yang rapat dan terdefinisi dengan baik sebagai fungsi dari r m , dengan dispersi minimal, dan dapat ditangkap secara akurat menggunakan aproksimasi Padé dengan bentuk polinomial rasional yang sama seperti Persamaan ( 9 ). Perbandingan antara kecocokan Padé dan data asli (Gambar S9–S11 ) menunjukkan kesesuaian satu-satu yang sangat baik, yang mengonfirmasi keandalan kecocokan di seluruh ansambel PSD.

Gambar 7 berfungsi sebagai contoh seberapa baik aproksiman Padé sesuai dengan data binned. Secara khusus, gambar tersebut menunjukkan bagaimana aproksiman untuk band 3 (dari Tabel 2 dan 3 ) mereplikasi data binned. Seperti yang dapat dilihat dari gambar, kecocokan secara akurat menggambarkan data binned. Pada Gambar 7 , ada 1026 titik yang diplot sehingga dapat dilihat pada plot bahwa jumlah outliernya kecil. Namun, perlu dicatat bahwa data binned agak bising; ini mungkin karena bimodalitas yang lebih kuat di CASIM PSD. Namun, jumlah titik bising kecil, dan dengan demikian, mereka tidak akan mengurangi keakuratan kecocokan Padé.

Keakuratan Padé yang sesuai untuk setiap pita, seperti yang ditunjukkan pada Tabel 2 dan 3 , dinilai menggunakan koefisien determinasi ( r2 ) dan akar kuadrat rata-rata (rms). Rata-rata, nilai r2 di seluruh enam pita gelombang pendek untuk koefisien kepunahan massa dan parameter asimetri masing-masing adalah 99,72% dan 98,96%. Untuk pita yang tidak menyerap (yaitu, pita 1 dan 2), kesalahan dalam co-albedo dievaluasi menggunakan rms, yang ditemukan kurang dari 10−6 . Ini karena nilai co-albedo pada pita yang tidak menyerap ini sangat kecil, menjadikan r2 metrik yang tidak cocok untuk kasus seperti itu. Untuk empat pita gelombang pendek yang menyerap, nilai r2 rata-rata untuk co-albedo adalah 97,62%.

Untuk pita gelombang panjang, nilai r 2 rata-rata di seluruh sembilan pita untuk koefisien kepunahan massa, ko-albedo, dan parameter asimetri masing-masing adalah 99,65%, 96,99%, dan 98,99%. Hasil ini menunjukkan bahwa kecocokan Padé memberikan parameterisasi yang cukup akurat untuk tujuan penelitian ini.

Bagian berikutnya akan menguraikan dan membahas dampak penggunaan parameterisasi konsisten yang digabungkan dalam model regional.

6 DAMPAK DARI PARAMETRISASI YANG KONSISTEN TERPASANG PADA BIDANG RADIASI DALAM MODEL REGIONAL
Simulasi yang disajikan dalam bagian ini menggunakan studi kasus Darwin yang sudah ada yang telah digunakan untuk mengevaluasi berbagai konfigurasi CASIM dan model regional operasional terhadap pengukuran gelombang pendek dan panjang CERES (Clouds and Earth’s Radiant Energy System, lihat Loeb et al ., 2016 untuk informasi lebih lanjut tentang CERES). Dalam perbandingan ini, iradiasi gelombang pendek dan panjang yang keluar di TOA dibandingkan dengan produk CERES 1° per jam (yaitu, 10.5067/TERRA+AQUA/CERES/SYN1DEG-1HOUR_L3.004A ). Hasil perbandingan disajikan dalam Gambar 8 , di mana histogram untuk semua situasi langit diproduksi dengan menyajikan sekitar 60 hari keluaran T  + 27 dari 0Z (sekitar tengah hari setempat) sebagai histogram, dengan hari-hari yang berdekatan. Hasil menggunakan model atmosfer-daratan regional operasional berikutnya dari Kantor Meteorologi yang disebut ral3.1 dengan parametrisasi optik es saat ini juga ditunjukkan pada Gambar 8 .

Hasil gelombang pendek yang ditunjukkan di panel atas Gambar 8 menunjukkan bahwa parametrisasi konsisten baru yang digabungkan CASIM (ditunjukkan sebagai garis hijau dan merah penuh pada gambar) mereplikasi ujung iradiasi tinggi dari pengamatan gelombang pendek CERES (ditunjukkan sebagai garis hitam penuh pada gambar) lebih baik daripada parametrisasi optik es arus momen tunggal (ditunjukkan sebagai garis biru penuh pada gambar) yang dijelaskan dalam Baran et al . ( 2016 ). Untuk iradiasi antara 800 dan 1000 W·m −2 , hasil rata-rata spektral menggunakan parametrisasi dua momen yang konsisten mencapai Indeks Kesepakatan sebesar 0,74 (Willmott, 1981 ), yang menunjukkan kesepakatan yang umumnya baik dengan pengamatan. Sementara parametrisasi cenderung melebih-lebihkan jumlah piksel relatif terhadap pengamatan, perkiraan berlebihan ini berkurang secara signifikan dibandingkan dengan parametrisasi momen tunggal. Memang, parametrisasi momen tunggal secara signifikan melebih-lebihkan jumlah piksel relatif terhadap pengamatan, menghasilkan Indeks Kesepakatan hanya 0,32, yang menunjukkan kesepakatan yang buruk. Sebaliknya, parametrisasi dua momen yang konsisten meningkatkan ini secara signifikan, dengan demikian memberikan representasi yang lebih akurat dari distribusi yang diamati pada ujung iradiasi tinggi. Hasil gelombang panjang, ditunjukkan pada panel bawah Gambar 8 , menunjukkan kesepakatan yang sangat baik antara pengukuran CERES dan simulasi parametrisasi gabungan baru yang konsisten dengan CASIM. Secara khusus, pada ujung iradiasi rendah dari rentang gelombang panjang (<150 W·m −2 ), hasil rata-rata spektral mencapai Indeks Kesepakatan 0,97, yang menangkap tren yang diamati dengan deviasi minimal. Namun, ketika menggunakan ral3.1 dengan Baran et al momen tunggal . ( 2016 ) parameterisasi optik es, Indeks Kesepakatan yang ditemukan untuk parameterisasi momen tunggal adalah 0,91 untuk iradiasi <150 W·m −2 . Namun, pemeriksaan visual pada panel bawah Gambar 8 mengungkapkan perbedaan yang jelas dalam bentuk distribusi relatif terhadap pengamatan. Secara khusus, parameterisasi momen tunggal melebih-lebihkan jumlah piksel iradiasi rendah dan menunjukkan gradien yang kurang realistis, yang tidak sepenuhnya ditangkap oleh metrik Indeks Kesepakatan. Sebaliknya, skema dua momen mengikuti distribusi yang diamati secara dekat, baik dalam besaran maupun bentuk, menghasilkan Indeks Kesepakatan yang lebih tinggi sebesar 0,97 dan kesepakatan yang secara kualitatif lebih unggul.

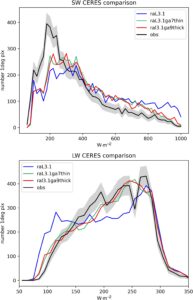
Perlu dicatat dari Gambar 8 bahwa perbedaan antara teknik perataan spektral ‘tipis’ dan ‘tebal’ kecil. Oleh karena itu, hasil hanya akan disajikan untuk kasus perataan spektral ‘tebal’, mengikuti rekomendasi Hogan dan Matricardi ( 2022 ).

Pengukuran iradiasi gelombang pendek dan panjang CERES memberikan wawasan tentang sifat kedalaman optik awan. Dalam histogram gelombang pendek, iradiasi TOA yang lebih tinggi (800–1000 W·m −2 ) biasanya menunjukkan reflektivitas awan yang lebih besar yang terkait dengan awan yang lebih tebal secara optik atau fraksi awan yang lebih tinggi, sedangkan dalam histogram gelombang panjang, iradiasi yang lebih rendah (<150 W·m −2 ) umumnya sesuai dengan puncak awan yang lebih tinggi dan lebih dingin dengan kedalaman optik yang lebih besar yang memerangkap radiasi termal yang keluar secara lebih efektif.

Gambar 9 menunjukkan hasil radiasi yang diperoleh di sekitar Inggris menggunakan rata-rata spektral ‘tebal’. Sekali lagi, produk CERES 1° per jam digunakan, di mana histogram untuk semua situasi langit diproduksi dengan menyajikan sekitar 40 hari keluaran T  + 27 dari 12Z (sekitar tengah hari setempat) sebagai histogram, dengan 40 hari tersebut berdekatan. Yang ditunjukkan pada Gambar 9 adalah perbandingan antara pengamatan CERES dan model regional operasional Met Office saat ini yang disebut ra2m dengan Baran et al . ( 2016 ) parameterisasi momen tunggal, ditunjukkan sebagai garis biru solid, CASIM dengan parameterisasi konsisten yang digabungkan ditunjukkan sebagai garis hijau solid, dan sama tetapi dengan Baran et al . ( 2016 ) parameterisasi ditunjukkan sebagai garis merah solid.

Kami juga membandingkan efek parametrisasi baru dengan hasil yang menggunakan Baran et al . ( 2016 ). Hasil yang disajikan dalam Gambar 9 menunjukkan bahwa dalam pita gelombang pendek (panel kiri), kesesuaian parametrisasi optik es konsisten yang digabungkan CASIM dengan pengukuran CERES lebih baik daripada optik es dalam ra2m, yang menggunakan Baran et al . ( 2016 ), dan parametrisasi optik es CASIM juga dari Baran et al . ( 2016 ). Parametrisasi optik CASIM konsisten yang digabungkan menangkap puncak pengukuran gelombang pendek CERES dan secara umum berada dalam ketidakpastian Poisson pada rentang histogram. Di wilayah gelombang pendek, parametrisasi dua momen (casim3p1_rad) mencapai Indeks Kesepakatan sebesar 0,95, yang menunjukkan kesepakatan yang kuat dengan distribusi yang diamati pada rentang histogram. Sebaliknya, model operasional saat ini (ra2m) mendapat skor lebih rendah, dengan Indeks Kesepakatan sebesar 0,87. Hasil ini memperkuat peningkatan kesetiaan parameterisasi dua momen dalam merepresentasikan distribusi radiasi gelombang pendek yang diamati.

Namun, dalam pita gelombang panjang (panel kanan), kita melihat bahwa parametrisasi optik CASIM konsisten yang digabungkan terlalu transmisif dan tidak cukup transmisif pada ujung iradiasi yang lebih tinggi dan lebih rendah dari pengukuran CERES, masing-masing. Dalam rentang iradiasi gelombang panjang 140–260 W·m − 2 , yang mencakup puncak distribusi radiasi gelombang panjang keluar yang diamati, parametrisasi momen tunggal (ra2m) mengungguli skema dua momen (casim3p1_rad) dalam hal kesepakatan dengan pengamatan. Secara khusus, Indeks Kesepakatan untuk parametrisasi momen tunggal adalah 0,74, dibandingkan dengan 0,60 untuk parametrisasi dua momen. Perbedaan ini konsisten dengan perkiraan berlebihan emisi yang terlihat pada Gambar 9 , di mana skema dua momen memprediksi lebih banyak piksel iradiasi tinggi di dekat puncak distribusi. Alasan untuk hasil gelombang panjang ini bisa jadi karena awan tidak berada pada ketinggian yang benar atau kesalahan dalam fraksi awan, dan/atau PSD terlalu sempit di wilayah ini. Parameterisasi momen tunggal Baran et al . ( 2016 ) lebih mengikuti PDF pengukuran CERES dalam gelombang panjang, tetapi ini kemungkinan besar karena pembatalan kesalahan.

Perbandingan menyeluruh antara pengukuran CERES dan simulasi parameterisasi CASIM konsisten yang digabungkan baru ditingkatkan melalui radiasi momen tunggal, dengan kesepakatan yang sangat baik pada ujung iradiasi rendah dari hasil gelombang panjang, ujung yang lebih tinggi dari hasil gelombang pendek, dan dalam kasus di sekitar Inggris, kesepakatan dengan pengukuran CERES secara umum baik dalam pita gelombang pendek. Jelas, hasil menyeluruh menunjukkan bahwa dengan secara konsisten menggabungkan optik es dengan mikrofisika dua momen, medan radiasi disimulasikan dengan lebih baik ketika perbandingan dilakukan dengan pengukuran berbasis ruang angkasa. Hanya dengan konsistensi seperti itu kita dapat berharap untuk mengurangi ketidakpastian dalam efek radiasi sirus.

7. DISKUSI DAN KESIMPULAN
Pekerjaan yang disajikan dalam makalah ini didasarkan pada model ensemble kristal es cirrus, yang menghasilkan tabel pencarian dua momen yang sepenuhnya konsisten dari sifat optik es curah di 170 panjang gelombang, berkisar dari 0,175 hingga 100 μm. Tabel pencarian ini digunakan untuk mengembangkan parameterisasi konsisten gabungan baru dari optik es curah berdasarkan masukan dua momen dari CASIM. Masukan dua momen ke parameterisasi mencakup rasio pencampuran massa es dalam awan total dan jumlah, yang digabungkan untuk memperoleh massa kristal es rata-rata per kristal es.

Dari massa kristal es rata-rata per kristal es, jari-jari bulat ekuivalen massa diturunkan, yang memiliki massa dan kepadatan padat yang sama dengan partikel nonsferis. Telah ditunjukkan bahwa mengekspresikan massa kristal es rata-rata per kristal es dalam bentuk jari-jari bulat ekuivalen massa secara akurat menggambarkan sifat optik es curah yang terkotak-kotak sebagai fungsi ukuran. Pendekatan ini memungkinkan penggunaan teknik aproksimasi Padé yang ada untuk menyesuaikan sifat optik es curah yang terkotak-kotak sebagai fungsi jari-jari bulat ekuivalen massa secara akurat. Teknik pemasangan ini, yang sebelumnya digunakan untuk parameterisasi tetesan air, telah diterapkan di sini untuk pertama kalinya untuk parameterisasi sifat optik kristal es. Perbedaan utama antara parameterisasi optik awan air dan kristal es adalah bahwa jari-jari efektif telah digantikan oleh jari-jari bulat ekuivalen massa untuk es. Keakuratan pemasangan sifat optik es curah yang terkotak-kotak untuk berkas spektral gelombang pendek enam pita standar dan berkas spektral gelombang panjang sembilan pita menggunakan aproksimasi Padé ditemukan cukup akurat untuk keperluan makalah ini. Makalah ini juga meneliti penggunaan teknik perataan spektral ‘tipis’ dan ‘tebal’ untuk optik es. Temuan makalah ini dapat diringkas sebagai berikut:

1. PSD CASIM dua momen dibandingkan dengan estimasi momen F07 pada Gambar  4 untuk normalisasi PSD di lintang tengah dan tropis pada berbagai suhu dan massa. Hasilnya menunjukkan bahwa PSD CASIM baru lebih baik dibandingkan dengan PSD F07, yang terkenal karena merepresentasikan PSD cirrus dan awan es.
2. Studi kasus Darwin all-sky, yang dilakukan selama 40 hari, menunjukkan bahwa parameterisasi optik es dua momen konsisten yang digabungkan meningkatkan kesesuaian dengan pengukuran gelombang pendek CERES, khususnya pada ujung iradiasi tinggi. Parameterisasi CASIM yang baru ditemukan lebih sesuai dengan pengukuran CERES daripada parameterisasi optik es momen tunggal Baran et al . ( 2016 ). Kesimpulan ini juga berlaku untuk pengukuran gelombang panjang.
3. Teknik perataan spektral ‘tipis’ dan ‘tebal’ dievaluasi dalam studi kasus Darwin, dan tidak ditemukan perbedaan yang signifikan. Hasilnya, simulasi model regional di seluruh Inggris dilakukan menggunakan teknik perataan spektral ‘tebal’, mengikuti rekomendasi Hogan dan Matricardi ( 2022 ).
4. Hasil di seluruh Inggris menggunakan rata-rata ‘tebal’ menunjukkan bahwa simulasi pengukuran gelombang pendek CERES menggunakan parameterisasi optik es konsisten yang digabungkan sangat sesuai dengan pengukuran tersebut. Namun, dalam pita gelombang panjang, parameterisasi baru agak terlalu transmisif dibandingkan dengan pengukuran CERES. Perbedaan ini dapat disebabkan oleh awan yang tidak berada pada ketinggian yang benar, kesalahan dalam fraksi awan, atau PSD yang terlalu sempit di wilayah ini.

Dalam makalah ini, kami telah menunjukkan bahwa penggabungan yang konsisten antara dua momen prognostik CASIM, yaitu massa dan jumlah, dan sifat optik es memiliki dampak yang sangat menguntungkan pada simulasi radiasi dalam model cuaca regional di berbagai belahan dunia. Pencapaian ini khususnya signifikan untuk wilayah yang diketahui bermasalah bagi model cuaca, seperti di sekitar Darwin, Australia, karena awan konvektif yang dalam dan cirrus semi-transparan yang terbawa oleh awan konvektif. Selain itu, konsistensi yang disajikan di sini tidak lagi menghalangi efek Twomey es analog yang penting untuk terjadi dalam CASIM, baik positif maupun negatif, dengan cara yang sama seperti yang terjadi pada awan cair. Di Met Office, kami sekarang dapat memasukkan aerosol dalam CASIM, tetapi sensitivitas radiasi terhadap penggabungan aerosol–es masih harus dipelajari nanti. Hanya melalui penggabungan yang konsisten antara mikrofisika dan radiasi menggunakan mikrofisika dua momen daripada mikrofisika momen tunggal, kami berharap dapat mensimulasikan efek radiasi cirrus secara lebih realistis dalam model cuaca dan iklim serta mengurangi ketidakpastiannya. Selain itu, penggabungan yang konsisten seperti itu akan menghasilkan umpan balik radiasi yang lebih menarik yang tidak ditemukan dalam skema momen tunggal.