ABSTRAK
Dalam model regresi linier, metode kuadrat terkecil biasa (OLS) digunakan untuk memperkirakan koefisien regresi yang tidak diketahui. Akan tetapi, penaksir OLS dapat memberikan perkiraan yang tidak dapat diandalkan dalam model non-ortogonal. Artikel ini memperkenalkan penaksir bias campuran baru untuk mengatasi tantangan yang ditimbulkan oleh model non-ortogonal. Penaksir yang diusulkan diturunkan melalui kombinasi dua penaksir, yaitu penaksir Stein dan penaksir ridge. Sifat-sifat teoritis dari penaksir yang diusulkan dibahas. Selain itu, kami menyarankan metode estimasi untuk memperkirakan nilai parameter penyusutan untuk penaksir yang diusulkan. Kami membandingkan kinerja penaksir yang diusulkan dengan penaksir Stein, penaksir ridge dengan standar dan dua parameter ridge terbaik, dan penaksir kuadrat terkecil biasa. Evaluasi ini didasarkan pada kriteria kinerja galat kuadrat rata-rata, menggunakan studi simulasi dan dua aplikasi praktis yang terkait dengan dataset semen dan crock. Hasil studi simulasi dan aplikasi menunjukkan bahwa penaksir yang diusulkan berkinerja lebih baik daripada penaksir lain yang dipertimbangkan.
1 Pendahuluan
Model regresi adalah alat yang dikenal luas untuk memprediksi dan mengidentifikasi faktor-faktor yang memengaruhi perubahan dalam variabel respons. Di antara berbagai model regresi yang tersedia, yang paling sering digunakan adalah model regresi linier (LRM), yang menemukan aplikasi luas dalam bidang-bidang seperti kemometrika dan lainnya [ 1 – 5 ]. LRM terutama digunakan ketika variabel respons mengikuti distribusi normal. Pendekatan estimasi kuadrat terkecil biasa (OLS) digunakan untuk estimasi LRM. OLS sesuai ketika semua asumsi regresi terpenuhi. Asumsi-asumsi ini melibatkan kenormalan dan homoskedastisitas, tidak adanya korelasi di antara variabel penjelas dan sebagainya. OLS dapat menghasilkan hasil yang lebih unggul ketika asumsi-asumsi utama ini terpenuhi. Dalam konteks LRM, ada contoh-contoh di mana ketergantungan muncul di antara variabel penjelas. Fenomena ini, yang dikenal sebagai multikolinearitas, pertama kali dijelaskan oleh Frisch [ 6 ]. Dengan adanya multikolinearitas, estimasi OLS tidak memenuhi sifat penduga linier tak bias terbaik (BLUE). Akibatnya, estimasi regresi menjadi kurang akurat, terutama karena meningkatnya kesalahan standar [ 7 ]. Selain itu, estimasi OLS mungkin menghasilkan tanda yang salah, interval kepercayaan cenderung jauh lebih lebar dan uji T dan F tidak signifikan [ 7 ].
Dalam situasi yang dicirikan oleh multikolinearitas, metode estimasi bias sering kali lebih disukai daripada OLS. Banyak peneliti telah mengembangkan metode estimasi bias satu dan dua parameter dalam konteks ini. Estimator bias satu parameter pertama dikenal sebagai estimator Stein (SE), yang dikembangkan oleh James dan Stein [ 8 ]. Lebih lanjut, studi estimasi bias ini dilakukan oleh Massy [ 9 ], yang memperkenalkan estimator bias lain yang dikenal sebagai estimator regresi komponen utama (PCRE). Untuk mendapatkan estimasi yang lebih efisien, Hoerl dan Kennard [ 10 ] memperkenalkan estimator satu parameter lain dengan menggunakan parameter bias, yang dikenal sebagai estimator regresi ordinary ridge (ORRE). Estimator bias satu parameter lain, yang dikenal sebagai estimator kontraksi, T dikembangkan oleh Mayer dan Willke [ 11 ]. Swindel [ 12 ] mengembangkan estimator bias alternatif yang dinamakan ‘modified ridge regression estimator’ (MRRE) untuk mengatasi masalah multikolinearitas. Untuk mengatasi kekurangan estimator ridge, estimator bias lainnya, seperti estimator Liu (LE), estimator Liu-Type (LTE) dan lainnya, dikembangkan dalam literatur [ 13 , 14 ].
Untuk mengatasi masalah multikolinearitas, metode estimasi bias lain diperkenalkan sebagai alternatif untuk estimator satu parameter yang dikenal sebagai estimator dua parameter (TPE). Salah satu keuntungan TPE dibandingkan estimator satu parameter adalah bahwa ketika parameter bias meningkat, mean squared error (MSEs) dari estimasi menurun [ 15 ]. Banyak peneliti telah memberikan kontribusi signifikan terhadap pengembangan TPE untuk LRM. Seperti Ullah dan Ullah [ 16 ] memperkenalkan double-penaksir kelas, Nomura dan Okhubo [ 17 ] membandingkanpenaksir kelas dengan ORRE dan penaksir OLS (OLSE), dan Sarkar [ 18 ] mengusulkan penaksir baru dengan menggabungkan metode estimasi ORRE dan metode estimasi kuadrat terkecil terbatas. Kaciranlar dan Sakallioglu [ 19 ] merekomendasikan penaksir kelas dengan ORRE dan penaksir OLS (OLSE), dan Sarkar [ 18 ] mengusulkan penaksir kelas dengan menggabungkan metode estimasi ORRE dan metode estimasi kuadrat terkecil terbatas.Penaksir kelas d , Sakallioglu et al. [ 20 ] melakukan studi perbandingan beberapa TPE yang bias, Ozkale dan Kaciranlar [ 21 ] mengembangkan TPE terbatas dan tidak terbatas, Sakallioglu dan Kaciranlar [ 22 ] mengembangkan TPE rpenaksir kelas d , Yang dan Chang [ 23 ] mengusulkan TPE baru, Chandra dan Sarkar [ 24 ] mengembangkan r terbatasEstimator kelas k dalam model regresi campuran, Roozbeh dan Arashi [ 25 ] mengusulkan TPE yang dimodifikasi, Dorugade [ 26 ] mengusulkan TPE yang efisien, Chandra dan Sarkar [ 27 ] menyajikan studi perbandingan estimator kelas r − (k,d) dengan beberapa estimator lain, Roozbeh [ 28 ] mempelajari estimasi berbasis QR optimal dalam LRM parsial, Lukman et al. [ 15 ] mengembangkan estimator m tipe ridge yang dimodifikasi dengan dua parameter dan baru-baru ini, Dawoud dan Kibria [ 29 ] memperkenalkan estimator Dawoud Kibria (DKE) untuk LRM.
Metode estimasi bias umumnya digunakan dalam kemometrika untuk pemodelan prediktif, yang mencakup tugas regresi dan klasifikasi. Khususnya, pemodelan prediktif memegang peran penting dalam beragam aplikasi. Dalam domain ini, ahli kemometrika telah merancang metodologi mereka yang didasarkan pada penalaran heuristik dan prinsip intuitif. Dalam kasus di mana regresor menunjukkan kolinearitas tinggi, ahli kemometrika sering beralih ke teknik seperti PCRE, partial least squares, dan regresi ridge. Metode-metode ini khususnya lazim dalam aplikasi data praktis dalam bidang kemometrika. Oleh karena itu, menjadi persyaratan untuk menggunakan teknik khusus yang secara efektif dapat mengurangi efek buruk kolinearitas, memastikan hasil pemodelan yang lebih kuat dan akurat. Penekanan pada penanganan regresor kolinear ini menggarisbawahi pentingnya pendekatan yang disesuaikan dalam domain kemometrika. Banyak penulis telah meneliti metode estimasi bias untuk berbagai model dan menunjukkan signifikansinya dalam bidang kemometrika. Vigneau dkk. [ 30 ] melakukan analisis komparatif dari PCRE, ORRE dan PCR-ridge estimator dalam konteks kalibrasi spektroskopi. Gusnanto et al. [ 31 ] menilai kinerja RRE dan metode partial least square untuk pemilihan variabel dalam model kalibrasi. Ngo et al. [ 32 ] menerapkan ORRE untuk mengatasi masalah multikolinearitas dalam studi kesetimbangan fase. Algamal [ 33 ] memperkenalkan RRE untuk model respons gamma, menggarisbawahi signifikansinya dalam bidang ilmu kimia. Lukman et al. [ 34 ] mengembangkan estimator tipe ridge yang dimodifikasi yang disesuaikan untuk LRM dan menggambarkan pentingnya menggunakan data yang terkait dengan semen Portland. Karlsson et al. [ 35 ] memperkenalkan LE untuk model beta dan menunjukkan relevansinya dengan bantuan kumpulan data yang terkait dengan hasil bensin dan warna hazelnut. Qasim et al. [ 36 ] mengusulkan beberapa parameter bias untuk estimator regresi ridge beta dan mengimplementasikannya dalam konteks data hasil bensin.
Dalam artikel ini, kami memperkenalkan estimator c − k (CKE) untuk mengurangi dampak masalah multikolinearitas dalam LRM. Studi ini berfokus pada CKE, yang menggabungkan estimator James Stein (JSE) [ 8 ] dan ORRE [ 10 ]. Lebih jauh, kami memperoleh sifat MSE dari CKE dan membahas sifat teoritis mengenai kinerjanya. Studi ini juga membuat perbandingan teoritis antara estimator yang diusulkan, OLSE, ORRE dengan ridge standar serta parameter ridge terbaik dan JSE, dengan melakukan eksperimen Monte Carlo dalam skenario yang berbeda, di mana MSE dan MSE matriks (MMSE) dianggap sebagai kriteria kinerja. Dua aplikasi praktis dalam bidang kemometrika, yang memanfaatkan estimasi bias untuk mengatasi tantangan non-ortogonal dalam LRM, diperiksa untuk menggambarkan keuntungan dari metode yang diusulkan. Aplikasi ini melibatkan kumpulan data yang terkait dengan kumpulan data semen dan tempayan yang menunjukkan keunggulan estimator yang diusulkan dan yang sudah ada dalam mengatasi masalah yang disebutkan. Sisa artikel ini diuraikan sebagai berikut: Bagian 2 membahas CKE untuk LRM, properti MSE, dan aspek teoritis. Di Bagian 3 , kami menyajikan desain eksperimen dan hasil simulasi Monte Carlo. Bagian 4 menganalisis aplikasi dan menyoroti pemanfaatan berbagai penduga bias. Terakhir, Bagian 5 merangkum kesimpulan penelitian.
2 Metodologi Statistik
Mari kita perhatikan bentuk LRM berikut ini,




2.1 Estimator yang Diusulkan
Kinerja setiap estimator menjadi dua kali lipat dengan menggabungkan kedua estimator tersebut. Ketika parameter yang bias meningkat, MSE cenderung menurun [ 15 ]. Pada dasarnya, TPE direkomendasikan untuk meningkatkan akurasi estimasi parameter dalam LRM ketika menghadapi multikolinearitas yang parah. Jadi, untuk mengurangi efek buruk multikolinearitas, kami mengusulkan estimator bias baru yang dikenal sebagai CKE untuk LRM. Untuk berharap bahwa kombinasi dua estimator yang berbeda dapat mewarisi keuntungan dari kedua estimator, yaitu, CKE menggabungkan JSE [ 8 ] dengan ORRE [ 10 ] yang didefinisikan sebagai


2.2 Perbandingan Teoritis Estimator LRM Berdasarkan MMSE dan Skalar MSE

2.3 Pemilihan Parameter Bias untuk CKE
Pemilihan parameter bias memberikan kontribusi peran utama dalam estimator bias. Untuk tujuan ini, banyak penulis mempertimbangkan metode estimasi yang berbeda [ 7 , 10-12 , 15 , 26 , 39 ]. Kami mempertimbangkan parameter Stein sebagaimana telah didefinisikan dalam Persamaan ( 10 ) . ORRE juga didasarkan pada parameter ridge k , dan lebih dari 100 k diusulkan dalam literatur [ 40 , 41 ] . Dalam karya ini, kami mempertimbangkan tiga parameter ridge. Pertama, kami mempertimbangkan yang awalnya diusulkan oleh Hoerl dan Kennard [ 6 ] sebagai
![]()
Mermi et al. [ 41 ] mensurvei dan membandingkan kinerja 80 parameter ridge dengan bantuan studi simulasi di LRM dan melaporkan beberapa parameter ridge terbaik. Kami mempertimbangkan dua parameter ridge terbaik berikut sebagai

Mengikuti penaksir bias lainnya dengan usulan parameter biasnya dan pekerjaan yang diberikan oleh Mermi et al. [ 41 ], kami menyarankan nilai berikut untuk c dan k .
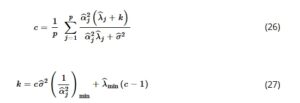
di mana ‘min’ menunjukkan nilai minimum dari ekspresi tersebut. Karena c dan k terlibat dalam Persamaan ( 26 ) dan ( 27 ), prosedur sistematis diperlukan untuk memperkirakan nilai-nilainya. Prosedur ini dapat dibagi menjadi beberapa langkah berikut:
- Awalnya, tentukan nilai c menggunakan Persamaan ( 26 ), dengan k seperti yang didefinisikan dalam Persamaan ( 16 ).
- Selanjutnya, tentukan nilai k dengan menggunakan Persamaan ( 27 ), berdasarkan nilai c yang diperoleh pada langkah (i).
- Selanjutnya hitung nilai c menggunakan Persamaan ( 26 ), dengan memperhitungkan nilai k yang diperoleh pada langkah (ii).
3 Studi Simulasi Monte Carlo

4 Desain Simulasi Monte Carlo
Pada subbagian ini, kami membandingkan kinerja sejumlah estimator, termasuk OLSE, JSE, ORRE dan CKE, menggunakan eksperimen simulasi Monte Carlo. Kami mengikuti desain simulasi yang sama dari eksperimen yang digunakan oleh Kibria [ 40 ] dan McDonald dan Galarneau [ 42 ]. Variabel penjelas yang berkorelasi dihasilkan sebagai berikut:

4.1 Hasil dan Pembahasan
MSE yang diestimasi dari berbagai estimator yang bias, termasuk OLSE, disajikan dalam Tabel 1–9 . Berbagai kondisi harus disertakan dalam studi simulasi untuk membandingkan kinerja CKE dengan estimator lainnya. Pembahasan umum tentang temuan simulasi disajikan di bawah ini:
- Korelasi antar regresor, yang merupakan faktor penting, jelas memengaruhi kinerja setiap estimator. Ketika kami memeriksa hasilnya, kami menemukan dari Tabel 1–9 bahwa ada hubungan langsung antara estimator dan tingkat multikolinearitas kecuali ORRE dengank2andk3. Meskipun parameter ridge ini diidentifikasi sebagai yang terbaik dalam karya Mermi et al. [ 41 ] tetapi memiliki MSE yang lebih kecil dibandingkan dengan yang lain. Untuk semua tingkat multikolinearitas, SRRE dengank2andk3memberikan kinerja yang lebih baik tetapi tidak memiliki pola multikolinearitas yang kompatibel seperti yang tersedia dalam literatur. Jadi, CKE berkinerja jauh lebih baik dibandingkan dengan metode estimasi lainnya. Dapat juga dilihat bahwa OLSE adalah estimator yang paling terpengaruh secara negatif dan peningkatan MSE OLSE entah bagaimana lebih besar daripada yang lain dengan meningkatkan tingkat korelasi.
- Peningkatan nilai ukuran sampel menghasilkan penurunan nilai MSE simulasi CKE serta estimator lainnya (lihat Tabel 1–9 ). Jadi, ukuran sampel memiliki dampak tidak langsung pada nilai MSE yang diestimasi. Untuk semua nilai n yang dipertimbangkan , kami melihat bahwa kinerja CKE lebih baik dibandingkan dengan OLSE, ORRE dengank1dan JSE ketika terdapat masalah multikolinearitas yang tinggi tetapi tidak sempurna.
- Kami juga membandingkan kinerja estimator dengan meningkatkan jumlah regresor. Dapat diamati dari temuan studi simulasi bahwa nilai MSE dari semua estimator meningkat dengan meningkatkan jumlah regresor (lihat Tabel 1–9 ) kecuali ORRE dengank2andk3Seperti yang diharapkan, CKE mengungguli OLSE, ORRE dengank1dan JSE untuk semua regresor yang dipilih. Selanjutnya, ORRE dengank2andk3berperforma lebih baik dibandingkan dengan OLSE, JSRE dan JSE karena tata letaknya yang tidak terlalu membengkak saat terjadi multikolinearitas tinggi.
- Karena kita telah mempertimbangkan tiga nilai yang berbeda,σ2, hasil Tabel 1-9 menunjukkan adanya peningkatan nilaiσ2, menyebabkan kenaikan bertahap pada nilai MSE yang diestimasikan. Untuk semua nilai MSE yang diestimasikanσ2, kita dapat melihat bahwa kinerja CKE secara konsisten menunjukkan pola yang lebih unggul dan lebih kuat dibandingkan dengan metode estimasi lainnya.
- Mengingat kita membandingkan kinerja CKE yang diusulkan dengan OLSE tradisional, ORRE dengan k standar dan dua k lainnya [ 41 ] dan JSE. Temuan kami menunjukkan bahwa ORRE dengank2andk3memberikan variasi yang lebih kecil, sedangkan pola mereka untuk faktor simulasi yang dipertimbangkan tidak sesuai dengan literatur. Khususnya, untuk multikolinearitas, seiring dengan peningkatan multikolinearitas, MSE dari estimator juga meningkat. Namun, MSE ORRE dengank2andk3tidak memiliki pola seperti itu (Lihat Tabel 1–9 ). Jadi, mengingat keterbatasan ini, kita dapat mengatakan bahwa CKE secara konsisten mengungguli estimator lain, khususnya dalam hal mencapai MSE yang lebih rendah (lihat Tabel 1–9 ). Kami juga mengamati bahwa OLSE mencapai MSE maksimum, yang menunjukkan bahwa OLS bukanlah pilihan yang tepat ketika ada multikolinearitas yang tinggi tetapi tidak sempurna. Sementara itu, dapat dilihat bahwa kinerja JSE bahkan lebih buruk ketika kita membandingkannya dengan ORRE. Namun, secara keseluruhan, kinerja CKE lebih baik dibandingkan dengan estimator lain yang dipertimbangkan dalam penelitian ini.
TABEL 1. Estimasi kesalahan kuadrat rata-rata (MSEs) untuk p = 4,σ2=0.5. N ρ Bahasa Inggris ATAU JSE JSRE k1 k2 k3 50 0,80 3.80 2.72 0,94 0,70 3.11 3.05 0,90 Jam 7.30 4.86 0.83 0.57 Tanggal 4.09 3.58 0,95 tanggal 14.16 9.12 0,79 0.62 5.68 4.79 0,99 71.84 44.84 0.71 0,88 tanggal 18.12 15.84 100 0,80 2.61 1.97 1.03 0.76 2.54 2.92 0,90 4.59 3.21 0.82 0.61 3.19 3.20 0,95 8.87 5.96 0,79 0.52 4.34 3.87 0,99 41.67 26.40 0.73 0,55 Tanggal 11.21 Tanggal 10.22 200 0,80 2.47 1.88 1.07 0,79 2.59 2.71 0,90 4.24 3.00 0.83 0.63 3.15 2.90 0,95 7.74 5.19 0.81 0.54 4.14 3.74 0,99 35.47 pukul 22.40 0.72 0.43 9.64 9.68 400 0,80 2.52 1.93 1.05 0,79 2.56 2.88 0,90 jam 4.30 3.04 0,88 0.67 3.16 3.14 0,95 7.86 5.28 0,77 0.51 4.07 3.87 0,99 36.37 22.93 0.71 0.36 9.65 9.78
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 60.83 | 40.61 | 3.33 | 3.58 | 33.00 | 24.35 |
| 0,90 | 117.97 | 75.49 | 3.17 | 3.26 | 64.11 | 46.21 | |
| 0,95 | 227.74 | 142.03 | 3.10 | 3.44 | 123.42 | 93.94 | |
| 0,99 | 1123.12 | 696.34 | 3.07 | 3.86 | 613.77 | 468.13 | |
| 100 | 0,80 | 41.74 | 28.54 | 3.48 | 3,99 | 22.49 | 16.35 |
| 0,90 | 71.68 | 47.02 | 3.01 | 3.20 | 38.01 | 28.89 | |
| 0,95 | 135.25 | 86.65 | 2.98 | 3.10 | 71.72 | 53.69 | |
| 0,99 | 668.02 | 421.77 | 2.95 | 3.28 | 360.03 | 264.08 | |
| 200 | 0,80 | 40.96 | 28.25 | 3.33 | 3.95 | 22.16 | 16.44 |
| 0,90 | 68.18 | 45.31 | 3.15 | 3.54 | 36.89 | 27.83 | |
| 0,95 | 120.45 | 77.24 | 2.93 | 3.01 | 63.93 | 46.43 | |
| 0,99 | 558.14 | 347.31 | 2.86 | 2.93 | 292.19 | 230.10 | |
| 400 | 0,80 | 39.87 | Jam 27.30 | 3.31 | 3.94 | 21.35 | 15.80 |
| 0,90 | 69.36 | 45.88 | 2,99 | 3.38 | 37.17 | Tanggal 28.05 | |
| 0,95 | 127.14 | 81.69 | 2.88 | 2.89 | 67.40 | 51.81 | |
| 0,99 | 252.68 | 168.40 | 4.87 | 6.14 | 175.59 | 125.58 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 247,00 | 163.41 | 4.63 | 5.83 | 169.73 | 122.85 |
| 0,90 | 458.46 | 290.30 | 4.75 | 5.71 | 314,98 dolar | 221.28 | |
| 0,95 | 899.60 | 557.90 | 4.63 | 5.24 | 620.31 | 452.80 | |
| 0,99 | 4403.59 | 2699.63 | 4.65 | 5.22 | 3049.31 | 2320.42 | |
| 100 | 0,80 | 168.37 | 114.38 | 4.65 | 6.60 | 113.76 | 78.44 |
| 0,90 | 290.55 | 190.07 | 4.68 | 6.32 | 198.08 | 145.19 | |
| 0,95 | 542.20 | 344.08 | 4.32 | 5.68 | 369,99 | 268.46 | |
| 0,99 | 2555.70 | 1592.16 | 4.55 | 5.13 | 1753.12 | 1244.49 | |
| 200 | 0,80 | 158.97 | 108.26 | 4.61 | 6.96 | 107.24 | 75.97 |
| 0,90 | 278.91 | 185.63 | jam 4.45 | 6.51 | 192.66 | 140.88 | |
| 0,95 | 487.29 | 311.35 | 4.33 | 5.43 | 332.66 | 228.08 | |
| 0,99 | 2294.51 | 1447.12 | 4.31 | 4.86 | 1586.86 | 1187.40 | |
| 400 | 0,80 | 163.38 | 111.58 | 4.39 | 6.71 | 111.49 | 77.28 |
| 0,90 | 272.20 | 178.23 | 4.21 | 6.36 | 185.48 | 134.55 | |
| 0,95 | 514,97 dolar AS | 332.76 | 4.39 | 5.90 | 355.21 | 256.75 | |
| 0,99 | 2423.68 | 1539.17 | 4.13 | 5.04 | 1683.35 | 1282.40 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 6.49 | 5.14 | 1.84 | 1.31 | 5.06 | 5.28 |
| 0,90 | tanggal 11.07 | 8.52 | 1.49 | 1.01 | 6.12 | 6.02 | |
| 0,95 | 20.52 | Tanggal 15.41 | 1.34 | 0.81 | jam 8.00 | 7.55 | |
| 0,99 | 94.07 | 69.48 | 1.19 | 1.36 | tanggal 21.11 | 18.90 | |
| 100 | 0,80 | 4.89 | 4.00 | 2.01 | 1.34 | 4.65 | 5.24 |
| 0,90 | 7.86 | 6.21 | 1.57 | 1.09 | 5.42 | 5.77 | |
| 0,95 | tanggal 14.06 | 10.90 | 1.33 | 0,80 | 6.62 | 6.71 | |
| 0,99 | 64.81 | 49.18 | 1.20 | 0,94 | 14.72 | 14.62 | |
| 200 | 0,80 | 5.73 | 4.68 | 1.74 | 1.19 | 4.78 | 5.67 |
| 0,90 | Tanggal 10.21 | 8.10 | 1.40 | 0,96 | 5.69 | Jam 6.30 | |
| 0,95 | 19.28 | tanggal 15.08 | 1.25 | 0.69 | 7.22 | 7.65 | |
| 0,99 | 93.06 | 72.08 | 1.15 | 0,59 | 18.93 | 19.25 | |
| 400 | 0,80 | 5.10 | 4.22 | 1.83 | 1.29 | 4.59 | 5.71 |
| 0,90 | 8.81 | 7.05 | 1.47 | 1.03 | 5.47 | Jam 6.30 | |
| 0,95 | 16.96 | 13.41 | 1.25 | 0,75 | 6.86 | jam 7.45 | |
| 0,99 | 80.48 | 62.53 | 1.15 | 0.42 | 16.52 | 16.94 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 106.57 | 81.73 | 5.63 | 5.57 | 55.01 | 41.04 |
| 0,90 | 180.60 | 136.48 | 5.19 | 5.14 | 93.17 | 68.13 | |
| 0,95 | 329.64 | 246.58 | 4.94 | jam 4.30 | 170.07 | 128.72 | |
| 0,99 | 1464.82 | 1066.75 | 4.50 | 5.75 | 732.54 | 541.93 | |
| 100 | 0,80 | 78.72 | 62.01 | 5.94 | 6.14 | 40.24 | Tanggal 29.20 |
| 0,90 | 125.33 | 96.64 | 5.44 | 4.84 | 62.90 | 45.81 | |
| 0,95 | 227.54 | 174.81 | 4.88 | 4.15 | Nomor 113.10 | 81.80 | |
| 0,99 | 1032.59 | 784.59 | 4.59 | 5.26 | 510.27 | 364.43 | |
| 200 | 0,80 | 91.41 | 72.07 | 5.48 | 5.51 | 45.71 | 32.38 |
| 0,90 | 161.79 | 125.63 | 5.05 | 4.35 | 79.79 | 57.49 | |
| 0,95 | 311.00 | 240.64 | 4.63 | 3.47 | 153.90 | 110.07 | |
| 0,99 | 1446.00 | 1108.67 | 4.59 | 4.57 | 697.68 | 496.45 | |
| 400 | 0,80 | 81.24 | 64.64 | 5.61 | 5.94 | 40.83 | 28.87 |
| 0,90 | 143.29 | 112.44 | 5.04 | 4.59 | 71.09 | 50.21 | |
| 0,95 | 271.24 | 211.39 | 4.73 | 3.58 | 133.62 | 94.93 | |
| 0,99 | 1256.59 | 966.20 | 4.66 | 3.86 | 603.30 | 427.74 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 421.11 | 323.12 | jam 7.40 | 9.69 | 282.59 | 201.96 |
| 0,90 | 717.49 | 539.72 | 7.26 | 8.59 | 484.66 | 339.21 | |
| 0,95 | 1306.59 | 973.36 | 6.86 | 7.92 | 884.15 | 646.69 | |
| 0,99 | 5973.31 | 4412.88 | 7.12 | 8.52 | 4060.86 | 2960.92 | |
| 100 | 0,80 | 311.50 | 243.45 | 7.56 | Jam 11.00 | 205.45 | 137.09 |
| 0,90 | 513.38 | 397.24 | 7.47 | 9.54 | 343.18 | 237.44 | |
| 0,95 | 897.17 | 683.00 | 7.16 | 8.38 | 594.14 | 413.78 | |
| 0,99 | 4174.02 | 3171.57 | 6.84 | 8.10 | 2785.81 | tahun 1920.73 | |
| 200 | 0,80 | 364.73 | 286.34 | jam 7.40 | 10.23 | 241.59 | 160.49 |
| 0,90 | 632.53 | 489.04 | 7.16 | 9.27 | 415.17 | 277.97 | |
| 0,95 | 1222.30 | 941.64 | 6.96 | 8.21 | Nomor telepon 808.02 | 550.68 | |
| 0,99 | 5828.31 | 4495.23 | 6.68 | 7.69 | 3874.34 | 2673.78 | |
| 400 | 0,80 | 327.01 | 260.03 | 7.51 | 11.96 | 217.85 | 144.74 |
| 0,90 | 564.32 | 441.10 | 7.03 | 9.84 | 372.43 | 248.57 | |
| 0,95 | 1073.26 | 834.76 | 6.96 | 8.93 | 711.15 | 483.30 | |
| 0,99 | 5203.11 | 4036.04 | 6.51 | 7.36 | 3463.44 | 2341.10 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 12,99 dolar | 10.43 | 2.76 | 1.69 | 8.27 | jam 8.00 |
| 0,90 | 24.82 | 19.74 | 2.03 | 1.25 | 10.44 | 9.90 | |
| 0,95 | 47.45 | 37.34 | 1.80 | 1.09 | tanggal 14.22 | 13.39 | |
| 0,99 | 243.55 | 190.73 | 1.63 | 1.20 | 47.38 | 46.56 | |
| 100 | 0,80 | 12.72 | 10.54 | 2.35 | 1.50 | Tanggal 8.05 | 8.43 |
| 0,90 | 25.75 | Tanggal 21.15 | 1.91 | 1.11 | 10.16 | pukul 10.55 | |
| 0,95 | 50.95 | 41.42 | 1.70 | 0.76 | tanggal 14.06 | 14.73 | |
| 0,99 | 259.40 | 210.59 | 1.58 | 1.74 | 45.75 | 46.11 | |
| 200 | 0,80 | 8.60 | 7.35 | 2.63 | 1.71 | 7.20 | 8.19 |
| 0,90 | tanggal 16.18 | 13.68 | 1.97 | 1.32 | 8.46 | 9.34 | |
| 0,95 | 30.62 | 25.57 | 1.78 | 0,88 | 10.67 | 11.64 | |
| 0,99 | 152.39 | 126.91 | 1.61 | 0,58 | 27.90 | 30.21 | |
| 400 | 0,80 | 8.34 | 7.18 | 2.58 | 1.74 | 6.95 | 8.69 |
| 0,90 | Tanggal 15.25 | 12.98 | 2.00 | 1.37 | 8.16 | 9.72 | |
| 0,95 | Tanggal 29.21 | 24.71 | 1.76 | 0,98 | Tanggal 10.20 | 11.69 | |
| 0,99 | 139.06 | 116.80 | 1.58 | 0.47 | 25.44 | 27.39 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 209.47 | 166.95 | Tanggal 8.05 | 6.60 | 106.51 | 82.65 |
| 0,90 | 396.34 | 312.77 | 7.38 | 6.18 | 200.30 | 153.46 | |
| 0,95 | 765.90 | 599.20 | 6.69 | Jam 6.30 | 382.32 | 293.75 | |
| 0,99 | 3854.24 | 3018.98 | 6.39 | 7.25 | Tahun 1908.82 | 1478.16 | |
| 100 | 0,80 | 201.81 | 164.35 | 7.32 | 5.53 | Nomor 98.10 | 72.89 |
| 0,90 | 395.55 | 320.28 | 6.89 | 4.97 | 190.52 | Nomor 141.30 | |
| 0,95 | Nomor telepon 832.12 | 677.25 | 6.74 | 5.52 | 409.47 | 307.50 | |
| 0,99 | 4156.52 | 3362.85 | 6.51 | 8.31 | Tahun 2013.85 | 1484.37 | |
| 200 | 0,80 | 137.61 | 115.47 | 7.83 | 6.99 | 66.95 | pukul 48.30 |
| 0,90 | 253.07 | 211.15 | 7.13 | Tanggal 5.08 | 121.79 | 86.41 | |
| 0,95 | 498.08 | 414.83 | 6.75 | 4.56 | 239.49 | 169.56 | |
| 0,99 | 2398.81 | tahun 1992.69 | 6.37 | 5.35 | 1134.77 | Nomor telepon 804.06 | |
| 400 | 0,80 | 132.44 | 111.96 | 7.73 | 6.92 | 64.12 | 45.34 |
| 0,90 | 240.91 | 202.43 | 6.99 | 5.05 | 115.15 | 81.66 | |
| 0,95 | 470.32 | 396.11 | 6.64 | 4.35 | 226.36 | 157.21 | |
| 0,99 | 2216.31 | 1855.14 | 6.48 | 4.67 | 1046.16 | 723,99 dolar | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
| N | ρ | Bahasa Inggris | ATAU | JSE | JSRE | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| 50 | 0,80 | 835.52 | 662.10 | pukul 10.45 | 11.33 | 558.36 | 409.74 |
| 0,90 | 1605.47 | 1268.52 | tanggal 10.07 | 10.92 | 1089.67 | Nomor telepon 804.25 | |
| 0,95 | 3147.54 | 2463.44 | 9.54 | 10.73 | 2123.39 | 1588.70 | |
| 0,99 | 15.407,24 | 12.032,31 | 9.48 | 10.83 | 10.296,30 | 7688.06 | |
| 100 | 0,80 | 828.91 | 676.89 | 10.28 | 11.54 | 550.35 | 384.31 |
| 0,90 | 1585.50 | 1281.09 | 9.76 | 10.58 | 1036.61 | 723.65 | |
| 0,95 | 3208.35 | 2593.04 | 9.37 | 9.58 | 2110.42 | 1505.06 | |
| 0,99 | 16.085,58 | 12.997,76 dolar AS | 9.31 | 11.39 | 10.536,04 juta | 7389.04 | |
| 200 | 0,80 | 550.41 | 460.85 | 10.28 | 13.39 | 359.85 | 237.08 |
| 0,90 | 995.76 | 826.04 | 9.77 | 10.73 | 647.65 | 433.34 | |
| 0,95 | tahun 1971.42 | 1636.68 | 9.65 | 10.13 | 1292.88 | 861.88 | |
| 0,99 | 9696.50 | 8062.26 | 9.26 | Jam 10.00 | 6364.82 | 4276.68 | |
| 400 | 0,80 | 542.91 | 460.11 | 10.17 | 13.76 | 358.36 | 230.60 |
| 0,90 | 952.08 | 798.27 | 9.61 | 10.89 | 619.50 | 406.75 | |
| 0,95 | Tahun 1867.03 | 1569.67 | 9.19 | 9.69 | 1229.72 | 818.81 | |
| 0,99 | 8957.28 | 7508.38 | 9.41 | 9.65 | 5880.70 | 3897.75 | |
Singkatan: JSE, Penaksir James-Stein; JSRE, Penaksir Regresi James-Stein Ridge; OLSE, Penaksir Kuadrat Terkecil Biasa; ORRE, Penaksir Regresi Ordinary Ridge.
5 Aplikasi
Pada bagian ini, kami mengevaluasi kinerja CKE dengan bantuan aplikasi nyata yang terkait dengan ilmu kimia. Untuk tujuan ini, kami mempertimbangkan kumpulan data semen dan tempayan.
5.1 Data Semen

| Ketentuan | Bahasa Inggris | Bahasa Indonesia: RRE | JSE | JSRE | Bahasa Indonesia: VIF | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| Konstan | 62.4054 | 8.5870 | 0,0514 tahun | 0,0421 pukul 0,0421 | 27.6076 | 19.8238 | |
| x1 | 1.5511 | 2.1046 | 2.0399 | 1.7046 | 0.6862 | 1.7309 | 38.49 |
| x2 | 0.5102 | 1.0648 | 1.1878 | 1.2623 | 0.2257 | 0.8132 | 254.42 |
| x3 | 0.1019 | 0.6681 | 0.6496 | 0.4258 | 0,0451 | 0.4606 | 46.87 |
| x4 | -0,1441 | 0,3996 tahun | 0,5086 tahun | 0,5566 tahun | -0,0637 | 0.2288 | 282.51 |
| MSE | 4912.09 | 727.97 | 855.61 | 878.86 | 2173.07 | 538.12 | |
| Parameter bias | k = 0 | k1=0.0077 | k2=12.2304 | k3=51.2706 | c = 0,4424 = 0,4424 | c = 0,8822, k = 0,0022 | |
Singkatan: JSE, James-Stein Estimator; JSRE, James-Stein Ridge Regression Estimator; OLS, ordinary least squares VIF, faktor inflasi varians.
Tabel 10 menunjukkan estimasi koefisien dan MSE dari dataset semen. Estimasi koefisien OLSE, JSE, ORRE dan CKE dihitung menggunakan Persamaan ( 2 ), ( 6 ), ( 11 ) dan ( 17 ) secara berurutan. Akan tetapi, MSE OLSE, JSE, ORRE dan CKE dihitung menggunakan Persamaan ( 5 ), ( 9 ), ( 15 ) dan ( 22 ). Nilai estimasi parameter bias ridge yang digunakan dalam ORRE juga diberikan dalam Tabel 10. Akan tetapi, parameter Stein dari JSE diperoleh menggunakan Persamaan ( 10 ) dan ditemukan sebesar 0,4424. Parameter bias untuk CKE ditentukan sebagai berikut:
Dan
Hasil yang disajikan dalam Tabel 10 menunjukkan bahwa kinerja CKE adalah yang terbaik, terutama karena MSE yang diestimasi lebih rendah jika dibandingkan dengan metode estimasi lainnya. Lebih jauh, perlu dicatat bahwa OLSE memiliki kinerja terburuk di antara para estimator, terutama disebabkan oleh adanya multikolinearitas. Hal ini terbukti karena OLSE menghasilkan MSE yang diestimasi lebih besar daripada semua estimator lainnya. Hasil ini menunjukkan bahwa estimator yang diusulkan, CKE secara konsisten memberikan kinerja yang lebih unggul dibandingkan dengan estimator lainnya.
5.2 Data Crock

| Ketentuan | Bahasa Inggris | Bahasa Indonesia: RRE | JSE | JSRE | Bahasa Indonesia: VIF | ||
|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | |||||
| Konstan | -27.0076 | -0,0012 | -0,0154 | -0,0012 | -7.4680 | -0,0011 | |
| x1 | 0,0205 | -0,0482 | -0,0495 | -0,0481 | 0,0057 pukul 0,0057 | -0,0453 | 23.32 |
| x2 | -0,0028 | -0,0074 | -0,0075 | -0,0074 | -0,0008 | -0,0069 | 10.66 |
| x3 | 0,0148 pukul 0,0148 | 0,0276 hari | 0,0276 hari | 0,0276 hari | 0,0041 pukul 0,0041 | 0,0260 | 2.29 |
| x4 | 0,0005 | -0,0003 | -0,0003 | -0,0003 | 0,0001 | -0,0002 | 8.19 |
| x5 | 0,0888 | -0,1308 | -0,1250 | -0,1309 | 0,0246 pukul 0,0246 | -0,1232 | 3.05 |
| x6 | 0,0035 | 0,0034 pukul 0,0034 | 0,0034 pukul 0,0034 | 0,0034 pukul 0,0034 | 0,0010 | 0,0032 | 4.43 |
| MSE | 1908.48 | 336.22 | 367.85 | 1354.81 | 527.72 | 31.32 | |
| Parameter bias | k = 0 | k1=0.4788 | k2=49.445 | k3=0.0049 | c = 0,2765 | c = 0,9414, k = 0,1701 | |
Singkatan: JSE, James-Stein Estimator; JSRE, James-Stein Ridge Regression Estimator; OLS, ordinary least squares VIF, faktor inflasi varians.
Hasil dari dataset Crock disajikan dalam Tabel 11 , dalam konteks kemometrika. Dengan adanya multikolinearitas, OLSE menghasilkan estimasi parameter yang tidak stabil untuk penyerapan oksigen, sehingga sulit untuk menentukan hubungan sebenarnya antara penyerapan oksigen dan O2UP (penyerapan oksigen dalam miligram oksigen per menit). Estimasi koefisien untuk permintaan oksigen biologis cenderung negatif dan tinggi saat menggunakan metode tradisional. Namun, dengan mengadopsi metode yang diusulkan, CKE, yang menggunakan teknik regularisasi, menjadi mungkin untuk memperkenalkan istilah penalti yang mengurangi pengaruh variabel yang sangat berkorelasi. Jadi, stabilisasi estimasi koefisien ini meningkatkan interpretabilitas dan akurasi model. Analisis aplikasi ini menunjukkan bahwa CKE mengungguli metode estimasi lain dengan secara konsisten menghasilkan nilai MSE yang lebih rendah. Selain itu, OLSE gagal memberikan kinerja yang lebih baik dengan adanya multikolinearitas di antara variabel penjelas, karena menghasilkan MSE yang diestimasi lebih tinggi dibandingkan dengan semua estimator lainnya.
6 Kesimpulan
Artikel ini memperkenalkan estimator bias baru, yaitu, estimator Stein-Ridge, yang secara efektif mengatasi multikolinearitas dengan menggabungkan SE [ 8 ] dan estimator ridge [ 6 ]. Kinerja estimator yang diusulkan dievaluasi dibandingkan dengan estimator kuadrat terkecil biasa, SE dan estimator ridge menggunakan studi simulasi Monte Carlo, di mana MSE dianggap sebagai kriteria evaluasi kinerja. Studi simulasi dievaluasi dalam kondisi yang berbeda seperti ukuran sampel, jumlah variabel penjelas, varians residual dan tingkat multikolinearitas. Hasil simulasi menunjukkan bahwa ORRE dengan
memberikan MSE yang lebih kecil, tetapi polanya dengan parameter ridge ini untuk parameter simulasi yang dipertimbangkan tidak sesuai dengan literatur yang tersedia. Meskipun estimator yang diusulkan memberikan kinerja yang lebih baik dibandingkan dengan JSE, OLSE dan ORRE dengan parameter ridge standar karena polanya sesuai dengan literatur. Selain itu, kami juga mempertimbangkan dua aplikasi nyata yang terkait dengan kemometrika untuk menunjukkan keunggulan estimator yang diusulkan dibandingkan yang lain. Meskipun ORRE dengan
tidak memberikan kinerja yang baik dibandingkan dengan penduga yang diusulkan karena pola hasil simulasi yang tidak sesuai. Temuan ini menunjukkan bahwa penduga yang diusulkan memberikan kinerja yang lebih baik dibandingkan dengan penduga lain untuk mengatasi efek multikolinearitas dalam LRM.
