Abstrak
Kami menggunakan data dari wahana antariksa Magnetospheric Multiscale, Solar Orbiter, dan Cassini untuk mempelajari secara statistik overshoot magnetik pada guncangan haluan Bumi, guncangan antarplanet, dan guncangan haluan Saturnus. Ukuran overshoot magnetik menunjukkan korelasi positif yang jelas dengan bilangan Mach Alfenik dan ketergantungannya pada beta plasma hulu diselidiki. Kami menyajikan hubungan empiris terkini yang darinya bilangan Mach Alfenik dapat diperkirakan hanya dengan menggunakan data medan magnet melalui pengukuran overshoot magnetik. Overshoot magnetik dan bilangan Mach Alfenik dibandingkan dengan simulasi hibrida 2D dan pengamatan sebelumnya pada guncangan haluan Saturnus. Perbandingan dengan Saturnus menunjukkan sedikit pergeseran antara kumpulan data. Alasan pergeseran ini dibahas dan mungkin timbul dari berbagai metode untuk memperoleh bilangan Mach. Akhirnya, kami mengeksplorasi kemungkinan memperkirakan potensi guncangan silang dengan ekspresi teoritis menggunakan overshoot magnetik yang dihitung dari setiap guncangan, bilangan Mach, dan beta plasma.
Poin-poin Utama
- Perbedaan overshoot magnetik yang diamati pada guncangan antarplanet, guncangan Bumi, dan guncangan haluan Saturnus dipelajari dan dijelaskan
- Hubungan empiris antara overshoot magnetik dan bilangan Mach Alfven ditentukan
- Variabilitas overshoot sepanjang permukaan guncangan dalam simulasi hibrida 2D dibandingkan dengan pengamatan
1 Pendahuluan
Gelombang kejut tanpa tabrakan ada di mana-mana di alam semesta (Bykov & Treumann, 2011 ; Treumann, 2009 ). Studi tentang guncangan tanpa tabrakan astrofisika dan heliosfer penting untuk memahami proses mendasar yang bertanggung jawab atas percepatan partikel bermuatan dan pemanasan plasma. Dalam skala besar, guncangan berperilaku sebagai diskontinuitas dalam aliran plasma, memisahkan wilayah hulu supermagnetosonik dari wilayah hilir submagnetosonik. Namun, pada skala kinetik yang lebih kecil, simulasi dan pengukuran in situ yang dilakukan selama beberapa dekade terakhir menunjukkan lapisan transisi guncangan yang diperluas, yang terdiri dari berbagai wilayah. Dinamika ion sebagian besar menentukan berbagai wilayah lapisan transisi guncangan (Gedalin et al., 2018 ) dan sangat berbeda tergantung pada orientasi medan magnet hulu (Balogh & Treumann, 2013 ; Burgess & Scholer, 2015 ; Tidman & Krall, 1971 ). Kejutan dengan nomor Alfvén Mach
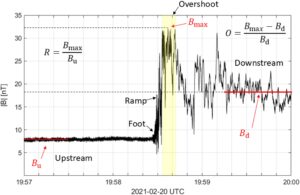
, yang secara umum disebut sebagai guncangan superkritis, berperilaku seperti sistem yang diredam secara kritis dan wilayah transisi biasanya mengandung medan magnet dan kelebihan kepadatan (Russell et al., 1982 ). Kelebihan tersebut terjadi tepat setelah tanjakan guncangan dan merupakan lokasi di mana kekuatan medan magnet dan kepadatan mencapai nilai maksimumnya di seluruh transisi guncangan (lihat Gambar 1 ). Sifat kelebihan tersebut terkait dengan ion yang secara langsung ditransmisikan melintasi guncangan, yang memperlambat aliran massal yang masuk (Balikhin et al., 2008 ; Gedalin & Sharma, 2023 ). Lebih jauh lagi, pembentukan overshoot memainkan peran penting dalam mengatur refleksi ion pada guncangan (Gedalin et al., 2022 ; Madanian et al., 2024 ; Russell et al., 1982 ; Sharma & Gedalin, 2023 ) karena panjang skala telah ditunjukkan baik oleh pengamatan dan simulasi berada di sekitar radius giro ion pantulan hulu (Leroy et al., 1982 ; Livesey et al., 1982 ). Perhitungan teoritis oleh Gedalin ( 2021 ) memprediksi ketergantungan overshoot pada bilangan Mach Alfvén, beta plasma hulu, dan potensi guncangan silang. Pengamatan selama beberapa dekade terakhir menunjukkan ketergantungan linear dari overshoot pada bilangan Mach dan sampai batas tertentu juga versus plasma beta pada berbagai kejutan busur planet yang berkisar dari Merkurius hingga Saturnus (Bohdan et al., 2021 ; Masters et al., 2013 ; Mellott & Livesey, 1987 ; Russell et al., 1982 ; Sulaiman et al., 2016 ). Sementara ketergantungan potensial kejutan silang pada bilangan Mach telah diselidiki dalam Dimmock et al. ( 2012 ), belum ada cukup data untuk memisahkan secara menyeluruh ketergantungan overshoot pada masing-masing dari tiga variabel yang disebutkan di atas. Sebagai aplikasi, hasil dan set data sebelumnya telah digunakan untuk menentukan bilangan Mach dari kejutan heliosfer di mana hanya data medan magnet yang tersedia (misalnya, Dimmock et al., 2022 , 2023 ). Namun, ini telah mengabaikan beta plasma eksplisit dan ketergantungan potensial kejutan silang pada overshoot.
Potensi guncangan silang memainkan peran penting dalam penataan guncangan dan karenanya juga overshoot guncangan (Gedalin et al., 2018 , 2023 ; Schwartz et al., 1988 ). Akan tetapi, tantangan teknis yang terkait dengan penentuan potensi guncangan silang menjadikan hakikat pasti potensi guncangan silang sebagai konsep yang masih kurang dipahami. Penelitian sebelumnya oleh Schwartz et al. ( 2021 ) mengevaluasi potensi guncangan silang menggunakan beberapa metode berbeda yang memanfaatkan pengukuran in situ. Metode-metode tersebut menunjukkan hasil yang sangat bervariasi dan cara yang paling akurat untuk menentukan potensi tersebut masih dalam perdebatan.
Dalam studi ini, kami melakukan analisis statistik ekstensif terhadap overshoot magnetik yang diukur secara in situ pada tiga jenis guncangan heliosfer yang berbeda, termasuk guncangan antarplanet (guncangan IP), guncangan busur Bumi, dan guncangan busur Saturnus. Kisaran luas dalam bilangan Mach yang diamati digunakan untuk mempelajari dan menentukan hubungan empiris antara overshoot magnetik dan bilangan Mach Alfvenik.
Peran dan ketergantungan pada beta plasma hulu
dan potensi guncangan silang ditinjau kembali dan dieksplorasi lebih lanjut. Lebih jauh, perbandingan antara berbagai jenis guncangan heliosfer dan metode yang digunakan untuk menghitung overshoot dibahas.
Perhatikan bahwa, untuk guncangan bilangan Mach tinggi, kami perkirakan permukaan guncangan dan transisi akan lebih bervariasi dan dipengaruhi oleh fenomena non-stasioner seperti riak dan reformasi (Johlander et al., 2016 , 2018 ; Madanian et al., 2021 ; Sulaiman et al., 2015 ). Oleh karena itu, kami perkirakan akan ada lebih banyak variabilitas dalam overshoot yang direkam oleh penyeberangan wahana antariksa tunggal saat bilangan Mach menjadi besar. Pekerjaan sebelumnya oleh Omidi et al. ( 2021 ) menunjukkan bahwa mungkin ada perbedaan besar antara profil guncangan spasial dan temporal (diukur oleh wahana antariksa) untuk bilangan Mach yang sangat besar, dan struktur guncangan tidak lagi dijelaskan oleh sub-wilayah berbeda yang diilustrasikan dalam Gambar 1 . Oleh karena itu, ketika membahas overshoot pada guncangan bilangan Mach tinggi, kami hanya merujuk pada kekuatan medan maksimum yang diukur di seluruh transisi guncangan relatif terhadap nilai hulu atau hilir (lihat Gambar 1 ). Kami mengeksplorasi variabilitas spasiotemporal dari overshoot ini dengan membandingkan sebaran statistik pada nilai observasi wahana antariksa tunggal dengan simulasi kinetik hibrida.
2 Data dan Metodologi
Sepanjang studi ini, kami akan menunjukkan kuantitas hulu dengan subskrip
dan kuantitas hilir dengan subskrip
, kuantitas yang berhubungan dengan spesies elektron dengan subskrip
, dan ion dengan subskrip
.
Overshoot magnetik dari guncangan kuasi-tegak lurus dapat didefinisikan dengan berbagai cara menggunakan besaran medan magnet hulu atau hilir. Gambar 1 menunjukkan besaran medan magnet dari guncangan yang melintas dari 20 Februari 2021 oleh wahana antariksa Magnetospheric Multiscale (MMS) dan mengilustrasikan dua definisi overshoot yang berbeda. Sebuah studi awal oleh Mellott dan Livesey ( 1987 ) menggunakan besaran medan magnet hilir,
, untuk menentukan amplitudo overshoot magnetik relatif menurut

2.1 Gempa Bumi
Overshoot magnetik, bilangan Mach Alfvénic, dan beta plasma dihitung menggunakan wahana antariksa MMS (Burch et al., 2016 ) untuk 444 persilangan guncangan busur Bumi. Kami menggunakan data medan magnet sampel 16 Hz dan momen plasma mode cepat yang diambil sampelnya pada 4,5 detik. Tiga ratus delapan puluh empat persilangan guncangan diperoleh dari basis data di Lalti et al. ( 2022 ) sementara 60 tambahan diambil dari studi oleh Lindberg et al. ( 2025 ). Dari basis data di Lalti et al. ( 2022 ), kami hanya mempertimbangkan yang diklasifikasikan sebagai kuasi-tegak lurus, yaitu, di mana medan magnet hulu membentuk sudut
terhadap guncangan normal. Persimpangan kuasi-tegak lurus ini disaring dengan memeriksa profil medan magnet, kepadatan, dan kecepatan massal secara manual di jendela
90an (kira-kira
ion terpantul (gyroradii) dari tanjakan kejut (menggunakan stempel waktu yang diberikan dalam basis data). Penyaringan mendeteksi klasifikasi palsu (struktur non-kejut) dan kasus-kasus non-ideal untuk penelitian. Kasus-kasus non-ideal mencakup lintasan kejut yang memerlukan interval waktu lebih panjang atau lebih pendek (dari 90 detik) di hulu atau hilir kejut dan kemudian dianalisis ulang menggunakan ukuran jendela waktu kejut yang lebih tepat. Klasifikasi palsu dibuang.
s sesuai dengan sedikit kurang dari
, dengan asumsi ion yang dipantulkan ke hulu sebesar 1 keV, kecepatan kejutan busur Bumi sebesar
km/s, dan
nT. Panjang interval waktu hulu dan hilir yang digunakan untuk merata-ratakan medan magnet, kepadatan, dan kecepatan ion ditetapkan sebesar 30 detik di hulu dan 45 detik di hilir, yang sesuai dengan kira-kira
Dan
ion gyroradii masing-masing (
nT). Suhu ion angin surya tidak diukur secara akurat oleh wahana antariksa MMS. Oleh karena itu, kami menggunakan data suhu ion OMNI 1 menit (King & Papitashvili, 2005 ) untuk menentukan beta plasma ion hulu untuk lintasan kejut MMS. Suhu ion ditentukan oleh rata-rata semua titik data terukur dalam interval waktu kejut yang dipilih untuk setiap kejut.
Angka Mach Alfven dihitung berdasarkan
![]()
Di mana
adalah kecepatan aliran plasma hulu dalam kerangka pesawat ruang angkasa,
kecepatan kejut,
kejutan normal, dan
kecepatan Alfvén di hulu. Normal guncangan untuk setiap guncangan diestimasikan menggunakan rata-rata dari tiga metode wahana antariksa mode campuran yang dijelaskan dalam Paschmann dan Daly ( 2008 ). Kecepatan guncangan diestimasikan menggunakan metode fluks massa dan Smith Burton (juga dijelaskan dalam Paschmann dan Daly ( 2008 )). Jika salah satu dari dua metode kecepatan guncangan menunjukkan tanda ketidakkonsistenan dengan pengamatan, metode tersebut dibuang, dan yang lain digunakan, jika tidak, rata-rata dari keduanya digunakan.
2.2 Guncangan Antarplanet (IP)
Kami menganalisis 37 penyeberangan guncangan IP menggunakan wahana antariksa Solar Orbiter (SolO) (Müller et al., 2020 ) dan produk data medan magnet mode burst 128 Hz (Horbury et al., 2020 ). Penyeberangan guncangan diperoleh dari database di Trotta et al. ( 2024 ). Sebagian besar penyeberangan IP menampilkan
Ini melengkapi kurangnya persimpangan kejut bernomor Mach rendah yang diamati di Saturnus dan kejut haluan Bumi. Kecepatan kejut IP jauh lebih cepat,
km/s, dan bervariasi jauh lebih banyak dibandingkan dengan lintasan busur bumi,
km/s saat diukur dalam kerangka wahana antariksa. Untuk memperlakukan analisis guncangan antarplanet pada pijakan yang sama dengan guncangan haluan Bumi, kami memutuskan untuk mencocokkan ukuran jendela waktu data untuk setiap guncangan IP yang melintasi
S
digunakan untuk kasus Bumi. Kami melakukan ini dengan memastikan bahwa interval waktu data guncangan IP sesuai dengan jumlah jari-jari giroskop ion pantulan hulu 1 keV yang sama
sebagai lintasan guncangan busur bumi. Oleh karena itu, ukuran jendela waktu untuk guncangan IP dipilih sesuai dengan
![]()
Di mana
mengacu pada radius giroskop ion terpantul 1 keV di hulu guncangan IP. Kekuatan medan hulu, hilir, dan maksimum kemudian diputuskan menggunakan interval waktu ini. Tanda lebih besar dari tetapi serupa dalam Persamaan 6 mengacu pada 30
aturan ditafsirkan sebagai nilai minimum. Mirip dengan studi guncangan busur Bumi, profil medan magnet untuk semua guncangan diperiksa secara manual untuk menghindari klasifikasi yang salah (kasus non-guncangan) dan deteksi pilihan awal yang tidak sesuai dari interval hulu dan/atau hilir. Guncangan ini kemudian dianalisis ulang dengan memilih interval hulu dan hilir yang sesuai secara manual untuk menghitung overshoot magnetik,
Dan
, Nomor Mach
, sudut kejut
dan kecepatan kejut
. Semua besaran guncangan IP lainnya diperoleh dari daftar guncangan di Trotta et al. ( 2024 ), misalnya ion plasma beta
Kuantitas basis data diperoleh dengan menggunakan teknik wahana antariksa tunggal yang dijelaskan dalam Paschmann dan Daly ( 2008 ) dengan menggunakan pendekatan berbasis ansambel jendela waktu rata-rata hulu dan hilir seperti yang dijelaskan dalam Trotta et al. ( 2022 ). Karena kurangnya pengukuran suhu elektron yang andal, kami memperkirakan beta plasma elektron
berdasarkan nilai rata-ratanya dalam angin matahari pada 1 AU dari Wilson et al. ( 2018 ). Hal ini menghasilkan
.
2.3 Guncangan Busur Saturnus
Studi kami mencakup 466 lintasan kejut haluan Saturnus yang diperoleh dari studi sebelumnya yang dilakukan oleh Sulaiman et al. ( 2016 ). Overshoot Saturnus dihitung menggunakan data medan magnet dari wahana antariksa Cassini (Matson et al., 2002 ). Sudut kejut
diperoleh sebagai sudut antara medan magnet lokal hulu dan normal kejut lokal yang diperoleh dari Went et al. ( 2011 ) sedangkan bilangan Mach diperoleh dengan memperkirakan tekanan ram hulu berdasarkan posisi pesawat ruang angkasa untuk setiap penyeberangan, lihat Sulaiman et al. ( 2016 ) dan Went et al. ( 2011 ) untuk deskripsi yang lebih rinci.
2.4 Simulasi Hibrida 2D
Kami melakukan simulasi Partikel-Dalam-Sel (PIC) kinetik-hibrida, di mana proton dimodelkan sebagai partikel (makro) sementara elektron diperlakukan sebagai cairan tak bermassa dan penetral muatan (Birdsall & Langdon, 1991 ). Kami menggunakan kode HYPSI, berdasarkan Metode Kemajuan Saat Ini dan algoritma Cyclic Leapfrog (CAM-CL) (Matthews, 1994 ). HYPSI menghasilkan rekonstruksi fidelitas tinggi dari perilaku guncangan pada skala kinetik ion, dengan kemungkinan memiliki inisialisasi dengan (Trotta, Pezzi, et al., 2023 ) dan tanpa (Trotta & Burgess, 2019 ) turbulensi hulu yang telah ada sebelumnya.
Metode injeksi (Quest, 1985 ) diadaptasi untuk menghasilkan kejutan, menyiapkan aliran plasma di
-arah dengan kecepatan (super-Alfvenik) yang ditentukan
Batas kanan domain simulasi bertindak sebagai dinding pemantul, sementara plasma terus menerus disuntikkan ke batas kiri. Simulasi bersifat periodik dalam
arah. Sebuah guncangan tercipta sebagai akibat dari refleksi di dinding, dan menyebar ke arah negatif
-arah. Dalam kerangka simulasi, aliran hulu (rata-rata) berada sepanjang normal kejut. Jarak dinormalkan ke panjang inersia ion
, waktu ke frekuensi siklotron terbalik
, kecepatan terhadap kecepatan Alfven
(semuanya mengacu pada keadaan hulu yang tidak terganggu), dan medan magnet dan kepadatannya mengacu pada nilai hulu yang tidak terganggu,
Dan
, masing-masing.
Simulasi yang disajikan di sini adalah 2,5 dimensi, dengan
domain dari
dan sebuah resolusi
= 0,5
Medan magnet hulu berada di
–
pesawat dan memiliki (nominal)
dari 45
Untuk kecepatan aliran hulu,
dipilih, dan bilangan Mach Alfvenik yang dihasilkan dari guncangan tersebut kira-kira
Fungsi distribusi ion hulu adalah Maxwellian isotropik dan beta plasma ion
Langkah waktu untuk kemajuan partikel adalah
= 0,01
Substepping digunakan untuk kemajuan medan magnet, dengan langkah waktu efektif
. Resistivitas kecil yang bukan nol diperkenalkan dalam persamaan induksi magnetik. Nilai resistivitas dipilih sedemikian rupa sehingga tidak ada fluktuasi yang berlebihan pada skala grid. Jumlah partikel per sel yang digunakan selalu lebih besar dari 400 (hulu), untuk menjaga karakteristik gangguan statistik simulasi PIC pada tingkat yang wajar.
2.5 Tingkat Pengambilan Sampel Pesawat Luar Angkasa dan Kecepatan Kejutan
Ketika mengukur overshoot magnetik dari lintasan kejut, seseorang perlu menentukan secara akurat kekuatan medan maksimum di seluruh lapisan transisi kejut. Keakuratan maksimum yang diukur ini akan bergantung pada dua parameter penting: laju pengambilan sampel pesawat ruang angkasa dan kecepatan kejut . Dengan kata lain, ada risiko bahwa
Dan
diukur lebih rendah dari nilai sebenarnya pada guncangan yang lebih cepat dan/atau tingkat pengambilan sampel pesawat ruang angkasa yang lebih rendah (Mellott & Livesey, 1987 ). Kami menyelidiki efek ini dengan memperkirakan jumlah titik data yang diukur,
, dalam overshoot kejut. Kami memperoleh jumlah titik data terukur menurut
![]()
Di mana
adalah frekuensi pengambilan sampel medan magnet pesawat ruang angkasa dan lebar spasial overshoot diasumsikan berada dalam urutan satu jari-jari giroskop ion yang dipantulkan di hulu
(Gedalin et al., 2018 , 2023 ; Leroy et al., 1982 ). Pertama, kami menggunakan 4 shock crossing dari set data MMS dan mengukur overshoot pada frekuensi sampling yang menurun mulai dari 8.200 Hz hingga 0,1 Hz menggunakan produk data medan magnet Fluxgate-Search coil Merged (FSM) (Le Contel et al., 2016 ; Russell et al., 2016 ). Tanggal, waktu, dan detail lainnya dari 4 contoh crossing ditabulasikan sebagai crossing no. 8, 9, 12, dan 22 dalam Tabel 1–3 di Lindberg et al. ( 2022 ). Jumlah titik data yang diukur,
, untuk setiap frekuensi pengambilan sampel, dalam overshoot dihitung. Perubahan fraksional overshoot sesuai dengan rasio overshoot yang diukur
pada frekuensi pengambilan sampel yang berbeda dan overshoot yang diukur pada laju pengambilan sampel tertinggi (8.200 Hz)
Kami mengamati bahwa perubahan fraksional overshoot
mulai berkurang seiring
turun di bawah 200, lihat Gambar 2a . Selanjutnya, kita hitung
untuk semua IP, Bumi, dan lintasan guncangan Kronian dalam kumpulan data kami, lihat Gambar 2b–2d . Perhatikan bahwa, tidak mungkin untuk mengukur kecepatan guncangan dari guncangan Kronian. Oleh karena itu, untuk Kronian
-nilai, kami mengasumsikan kecepatan kejut yang mirip dengan Bumi (
32 km/s). Kekuatan medan magnet hulu yang jauh lebih lemah di Saturnus meningkatkan
dibandingkan dengan Bumi. Namun, Sulaiman et al. ( 2016 ) menggunakan irama pengambilan sampel medan magnet yang lebih rendah, yaitu 1 Hz. Kedua efek ini menunjukkan bahwa persilangan guncangan Kronian harus diselesaikan dengan cara yang sama seperti di Bumi menggunakan MMS (bandingkan Gambar 2c dan 2d ).
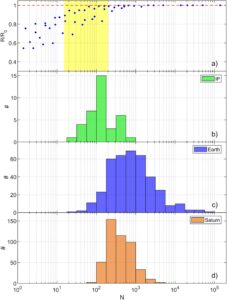
Gambar 2 memungkinkan kita untuk mengoreksi overshoot yang diukur pada guncangan dengan jumlah titik data overshoot yang rendah
Gambar 2a menunjukkan overshoot pada guncangan yang terjadi
(tanda kuning berbayang) yang akan mengalami koreksi. Overshoot pada guncangan yang memiliki
dikalikan dengan faktor 1,11 sedangkan kelebihan pada guncangan yang terjadi
dikalikan dengan faktor 1,20. Koreksi ini akan diilustrasikan dengan penggunaan simbol kotak hijau (guncangan IP) dan biru (guncangan busur Bumi). Kami akan menggunakan nomenklatur ini di seluruh naskah, di mana lingkaran menunjukkan data mentah dan kotak menunjukkan koreksi yang relevan.
Perhatikan bahwa overshoot kejut (dan lapisan transisi) diisi dengan fluktuasi medan magnet skala kecil. Fluktuasi magnetik ini akan ditumpangkan pada peningkatan medan magnet skala besar (biasanya disebut sebagai overshoot). Namun, dalam karya ini, kita akan mempertimbangkan fluktuasi gelombang skala kecil sebagai bagian dari overshoot magnetik. Hal ini didukung oleh hasil pada Gambar 2a , yang menunjukkan bahwa overshoot yang diukur lebih atau kurang konstan selama lebih dari dua
-puluhan tahun sebagai
(sesuai dengan laju pengambilan sampel di atas 100 Hz). Pada gilirannya, hal ini juga akan menyederhanakan analisis overshoot antara wahana antariksa (instrumen) yang berbeda pada guncangan heliosfer yang berbeda dengan selalu berupaya menggunakan laju pengambilan sampel tertinggi yang tersedia.
3 Analisis Statistik
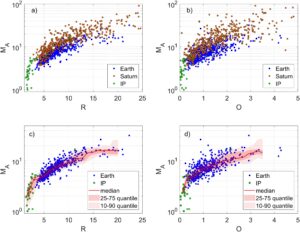
Gambar 3a dan 3b menunjukkan bilangan Mach Alfvén versus overshoot magnetik menggunakan tiga set data persilangan guncangan, Saturnus (oranye), Bumi (biru), dan guncangan IP (hijau). Perhatikan bahwa guncangan busur Kronian menunjukkan sedikit pergeseran ke arah bilangan Mach yang lebih tinggi dibandingkan dengan persilangan guncangan busur Bumi. Alasan pergeseran ini dibahas di bawah ini dalam Bagian 3.2 dan 4. Kami juga mengamati sebaran yang lebih besar saat menggunakan
definisi overshoot dibandingkan dengan
definisi. Gambar 3c dan 3d menunjukkan persimpangan IP dan guncangan Bumi dengan median dan batas kuantil 25% dan 10%. Pengamatan kami menunjukkan bahwa bilangan Mach Alfven mengikuti hubungan yang hampir linier dengan overshoot magnetik untuk
mirip dengan hasil sebelumnya oleh Mellott dan Livesey ( 1987 ) dan Russell et al. ( 1982 ). Untuk bilangan Mach yang lebih besar dari 10, kurva mulai mendatar sementara penyebaran overshoot meningkat. Efek ini diamati untuk persilangan guncangan Bumi dan Saturnus dan sesuai dengan hasil dari Madanian et al. ( 2024 ). Guncangan bilangan Mach rendah yang memiliki
didominasi oleh guncangan IP dan cenderung mengikuti kurva menurun ke arah
atau
.
Pada Gambar 4 , kami membandingkan data dari IP dan guncangan busur Bumi dengan ekspresi teoritis dalam Persamaan 3. Untuk menghubungkan bilangan Mach Alfvén hanya dengan overshoot yang diukur, beta plasma
dan potensi guncangan silang yang dinormalisasi
diperlakukan sebagai parameter bebas. Oleh karena itu, dari bentuk ekspresi analitis pada Persamaan 3 , kami mengasumsikan data mengikuti ekspresi serupa seperti
Di mana
Dan
adalah parameter yang sesuai untuk diperoleh. Perhatikan bahwa
parameter yang sesuai akan berhubungan dengan parameter potensi guncangan silang
sebagai
dan
parameter yang sesuai akan berhubungan dengan beta plasma sebagai
Kesesuaian terbaik, termasuk persimpangan IP dan busur kejut Bumi, ditunjukkan pada Gambar 4a dan diberikan oleh
![]()
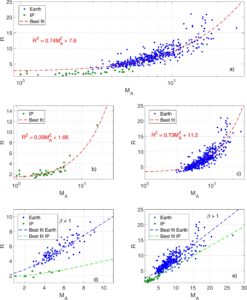
Tabel 1 menunjukkan ringkasan dari kecocokan terbaik, dengan mempertimbangkan juga persimpangan busur kejut IP dan Bumi secara terpisah dan untuk
dan beta plasma tinggi
.
| Ekspresi yang paling cocok | βJangkauan | Guncangan heliosfer |
|---|---|---|
| R2=0.74MA2+7.6 | 0.1<β<15 | Bumi dan IP |
| R2=0.73MA2+11.2 | 0.1<β<15 | Bumi (semua) |
| R2=0.14MA2+2.9 | 0.2<β<9 | IP (semua) |
| R2=0.12MA2+3.6 | 0.2<β<1 | AKU P(β<1) |
| R2=0.39MA2+3.44 | 1<β<9 | AKU P(β>1) |
| R2=0.80MA2+4.72 | 0.1<β<1 | Bumi(β<1) |
| R2=0.77MA2+6.84 | 1<β<15 | Bumi |
Catatan : Kecocokan dan data ditunjukkan pada Gambar 4 di bawah.
Kita melihat bahwa overshoot dan nomor Mach tampaknya mengikuti bentuk prediksi teoritis dalam Persamaan 3 dengan cukup baik tetapi untuk nilai koefisien yang berbeda antara IP dan lintasan Bumi, lihat Tabel 1 dan Gambar 4 di bawah ini. Namun, perlu dicatat bahwa nilai untuk parameter yang sesuai
tidak sepenuhnya sesuai dengan interpretasi sebagai
Selain itu, dua set data guncangan IP dengan
Dan
, masing-masing terdiri dari titik data yang relatif sedikit dan terdistribusi sedikit tidak merata di seluruh rentang bilangan Mach dan, oleh karena itu, tidak memiliki signifikansi statistik. Lebih jauh, beta plasma elektron yang tidak diketahui menimbulkan ketidakpastian besar mengenai apakah total beta plasma yang sebenarnya benar-benar kurang dari satu. Untuk menyelidiki kemungkinan perbedaan antara kedua jenis guncangan, kami menunjukkan pada Gambar 5 distribusi keseluruhan parameter guncangan untuk persilangan guncangan MMS (histogram biru) dan persilangan guncangan IP (histogram hijau). Perbedaan utama antara kedua jenis guncangan adalah bilangan Mach yang lebih rendah dan sudut guncangan yang lebih miring.
diamati pada guncangan IP dibandingkan dengan persimpangan guncangan haluan Bumi, lihat Gambar 5a dan 5b untuk nomor Mach dan Gambar 5e dan 5f untuk sudut guncangan. Namun, kami tidak menemukan ketergantungan yang kuat
dengan kemiringan guncangan (tidak ditampilkan), yang sesuai dengan penelitian sebelumnya (Dimmock et al., 2012 ; Sulaiman et al., 2016 ). Distribusi total beta plasma pada Gambar 5c dan 5d cukup mirip antara kedua jenis guncangan yang keduanya memuncak sekitar
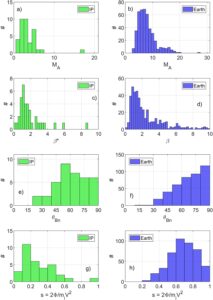
3.1 Potensi Guncangan Silang
Rumus yang menghubungkan kompresi overshoot dan bilangan Mach dalam Persamaan 3 juga melibatkan beta plasma dan potensi cross-shock yang dinormalisasi
Dengan rasio kompresi overshoot
, Nomor Mach
, dan plasma beta
diperoleh dari pengukuran pesawat ruang angkasa, kita dapat mencoba memperkirakan potensi guncangan silang yang dinormalkan pada overshoot guncangan
untuk setiap lintasan kejut. Gambar 5g dan 5h menunjukkan distribusi potensi kejut silang yang dihitung dan dinormalkan untuk lintasan kejut IP dan Bumi, masing-masing.
Kami menemukan bahwa estimasi potensi guncangan silang cenderung jauh lebih tinggi untuk lintasan guncangan busur Bumi dibandingkan dengan guncangan IP. Untuk Bumi, sebagian besar lintasan memiliki
dengan puncak sekitar
(Gambar 5h ). Sebagai perbandingan, guncangan IP memiliki
dengan puncak sekitar
(Gambar 5g ).
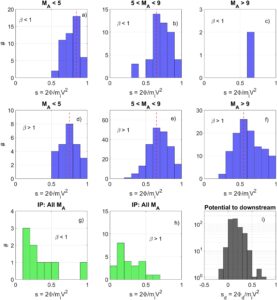
Kami menyelidiki lebih lanjut sifat-sifat potensi guncangan silang yang diperkirakan. Gambar 6 menunjukkan potensi guncangan silang yang dinormalisasi untuk tegangan rendah.
dan tinggi
plasma beta dan rentang yang berbeda dalam bilangan Mach. Gambar 6a–6f menunjukkan hasil untuk guncangan busur Bumi, Gambar 6g dan 6h menunjukkan hasil untuk guncangan IP, dan Gambar 6i menunjukkan potensi guncangan silang ke hilir
dengan menggunakan
pada Persamaan 3. Karena guncangan IP, beta elektron diambil sebagai nilai angin surya rata-rata di dekat
, kami hanya mempertimbangkan lintasan guncangan busur Bumi dan (empat) guncangan IP yang memiliki jarak heliosentris mendekati 1 AU
saat menghitung
Kami mengamati bahwa potensi guncangan silang hilir biasanya jauh lebih rendah daripada potensi guncangan silang pada titik overshoot. Beberapa persimpangan bahkan menunjukkan potensi negatif yang tidak fisik.
-nilai, kemungkinan besar menunjukkan keterbatasan ekspresi teoritis dalam Persamaan 3 .
.
Studi tentang distribusi potensi guncangan silang untuk rentang angka Mach yang berbeda pada Gambar 6a–6f menunjukkan bahwa puncak distribusi (ditunjukkan oleh garis putus-putus merah) bergerak ke nilai yang lebih rendah
untuk rentang nomor Mach yang lebih tinggi. Kami mengamati perilaku ini hanya untuk guncangan busur Bumi untuk kasus beta plasma tinggi dan rendah (tidak ada cukup guncangan IP untuk menarik
efek). Kami tidak mengamati perbedaan besar ketika mempelajari potensi guncangan silang IP-shock
untuk
lebih besar dan kurang dari 1 (Gambar 6g dan 6h ).
3.2 Bumi dan IP Versus Saturnus dan Simulasi
Pada Bagian ini, kami membandingkan data observasi kami dengan simulasi yang merekonstruksi perilaku guncangan dalam ruang dan waktu dan dengan demikian mengatasi keterbatasan penyeberangan tunggal (yang bersifat intrinsik pada observasi langsung) dengan menyelidiki variabilitas overshoot di sepanjang permukaan guncangan.
Hasil analisis ditunjukkan pada Gambar 7. Gambar 7b menunjukkan cuplikan simulasi yang menggambarkan transisi guncangan yang berkembang dengan baik. Terlihat jelas bahwa guncangan tersebut sangat tidak teratur dan dengan undulasi permukaan hingga beberapa puluh
skala, yang memainkan peran penting dalam perilaku keseluruhan kejutan (Kajdič et al., 2019 ; Krauss-Varban et al., 2008 ) serta percepatan partikel, lihat (Trotta, Horbury, et al., 2023 ) di mana simulasi ini digunakan untuk menjelaskan injeksi proton yang tidak teratur.

Pada Gambar 7a , serangkaian profil satu dimensi untuk tetap
ditunjukkan untuk transisi guncangan (garis berwarna), meniru 1.024 lintasan wahana antariksa pada guncangan. Dapat dilihat bahwa struktur overshoot menunjukkan tingkat variabilitas yang besar, juga dibandingkan dengan
-profil rata-rata yang ditunjukkan oleh garis hitam. Tingkat variabilitas tersebut dapat dikaitkan dengan variabilitas guncangan pada skala ion, sehingga persilangan guncangan lokal berpotensi sangat berbeda tergantung di mana guncangan tersebut dilintasi. Dalam simulasi,
dihitung sebagai berikut. Untuk setiap persimpangan, transisi guncangan diidentifikasi ketika besarnya medan magnet adalah 2,5 kali nilai hulunya
Di 5
hilir dari guncangan,
dihitung sebagai rasio antara besarnya medan magnet maksimum dan nilai hulu
Gambar 7c mengumpulkan histogram nilai overshoot
untuk semua penyeberangan untuk lebih mengkarakterisasi kompleksitas ini. Hal ini menunjukkan penyebaran yang signifikan di seluruh nilai overshoot
-6. Kami kemudian membandingkan hasil simulasi dengan penyeberangan MMS dengan yang serupa
dan plasma beta
Gambar 7d menunjukkan overshoot kompresi yang diamati
versus bilangan Mach
untuk penyeberangan yang memiliki
beserta rata-rata simulasi dan kesalahan standar. Hasil simulasi tampaknya tidak sepenuhnya sesuai dengan pengamatan. Baik overshoot rata-rata maupun variabilitasnya tampaknya lebih rendah daripada pengamatan statistik.
Seperti yang disebutkan di atas, Gambar 3 menunjukkan bahwa kumpulan data guncangan busur Kronian tampaknya bergeser ke arah angka Mach yang lebih tinggi untuk overshoot yang serupa dibandingkan dengan kumpulan data guncangan busur Bumi, lebih dari yang diharapkan dari rata-rata yang lebih tinggi.
rezim. Hal ini mungkin disebabkan oleh metode yang berbeda yang digunakan untuk menentukan bilangan Mach untuk lintasan kejut Kronian. Karena kurangnya data plasma yang sesuai,
di Saturnus diperkirakan berdasarkan lokasi wahana antariksa pada saat guncangan melintas untuk menentukan tekanan dinamis hulu dari model guncangan haluan yang ada, lihat Sulaiman et al. ( 2016 ) untuk keterangan lebih rinci. Sebuah studi sebelumnya oleh Jackman et al. ( 2019 ) menunjukkan bahwa tekanan dinamis hulu yang diperkirakan, yang diperoleh dengan menggunakan model guncangan haluan Went et al. ( 2011 ), sedikit dilebih-lebihkan dibandingkan dengan tekanan dinamis yang diperoleh dari monitor propagasi angin surya hulu (lihat Jackman et al. ( 2019 )). Selain itu, penelitian terbaru menggunakan pengamatan wahana antariksa MMS di guncangan haluan Bumi (Burkholder et al., 2025 ) menunjukkan bahwa penggunaan jenis metode ini memang melebih-lebihkan bilangan Mach Alfvén dengan faktor perkiraan sebesar 1,28
Oleh karena itu, kami menerapkan faktor koreksi ini pada kumpulan data Kronian. Hasilnya ditunjukkan pada Gambar 8. Perpotongan Kronian (kotak oranye) dan MMS (biru) kini terlihat sangat cocok.
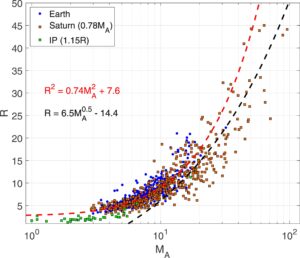
Studi simulasi sebelumnya yang dilakukan oleh Bohdan et al. ( 2021 ) mengamati overshoot magnetik pada suhu tinggi
guncangan dan menemukan bahwa kompresi overshoot
Garis hitam putus-putus pada Gambar 8 menunjukkan kesesuaian terbaik dari persimpangan kejut dengan
diberikan oleh
sedangkan garis putus-putus merah adalah ekspresi yang diperoleh pada Persamaan 8. Ekspresi hitam menggambarkan data lebih baik untuk bilangan Mach di atas 15.
4 Diskusi dan Kesimpulan
Definisi overshoot yang berbeda yang disajikan dalam Persamaan 1 dan 2 memiliki kelebihan dan kekurangannya sendiri. Overshoot relatif,
, bergantung pada pengukuran medan magnet hilir dan mungkin merupakan definisi yang paling logis mengingat ia mengukur seberapa besar kekuatan medan maksimum pada guncangan secara harfiah melampaui besarnya medan magnet hilir yang telah ditetapkan. Ini memberikan batas bawah yang intuitif
guncangan tanpa overshoot yang ada. Namun, karena fluktuasi medan magnet yang jauh lebih besar di hilir guncangan daripada di hulu, menggunakan definisi rasio kompresi overshoot dalam Persamaan 2 , cenderung menghasilkan kesalahan yang lebih sedikit. Kita dapat melihat ini dengan membandingkan Gambar 3a dan 3c dengan Gambar 3b dan 3d di mana sebaran data lebih besar untuk
definisi dibandingkan dengan
kompresi overshoot juga lebih umum digunakan dalam perhitungan teoritis dan karenanya menawarkan peluang untuk perbandingan dengan teori (Gedalin, 2021 ; Gedalin et al., 2018 ). Oleh karena itu, kami memfokuskan sebagian besar penelitian ini pada
definisi untuk overshoot magnetik. Misalkan karena alasan apa pun seseorang hanya boleh memiliki akses ke pengukuran hilir (atau pengukuran hulu yang tidak signifikan). Dalam hal itu, bilangan Mach Afven dapat diperkirakan menggunakan
definisi overshoot dan Gambar 3d .
Hasil dari Bagian 2.5 memberitahu kita untuk mengingat dua faktor penting ketika menentukan overshoot magnetik pada suatu guncangan: kecepatan guncangan dan laju pengambilan sampel pesawat ruang angkasa . Hasil dari penelitian ini setuju dengan kesimpulan yang ditemukan oleh Mellott dan Livesey ( 1987 ) yang memperoleh hubungan linier yang berbeda antara amplitudo overshoot relatifdan bilangan Alfven Machmenggunakan laju pengambilan sampel wahana antariksa yang berbeda. Akan tetapi, untuk kecepatan kejut yang substansial, parameter yang penting adalah jumlah titik data terukur dalam wilayah overshoot. Gambar 2 menunjukkan bahwa setidaknya diperlukan 200 titik data untuk mendapatkan estimasi overshoot magnetik yang akurat. Selain itu, seperti yang disebutkan dalam Bagian 2.5 , fluktuasi magnetik merupakan bagian yang konsisten dari lapisan transisi kejut dan biasanya ada dalam semua kejut. Oleh karena itu, kami menganggap fluktuasi sebagai bagian dari overshoot dan kami sarankan untuk menggunakan laju pengambilan sampel tertinggi yang tersedia saat menentukan overshoot.
Kecocokan terbaik yang berbeda yang diperoleh untuk lintasan IP dan guncangan Bumi pada Gambar 4 menunjukkan bahwa potensi guncangan silang yang berbeda secara rata-rata menggambarkan guncangan IP dan guncangan busur Bumi. Namun, potensi guncangan silang ditentukan melalui ekspresi analitis dalam Persamaan 3 , yang memiliki keterbatasan dan tidak boleh dianggap sebagai persamaan universal. Misalnya, ekspresi tersebut mengabaikan pemanasan elektron di seluruh guncangan dan sebagian besar refleksi ion (Gedalin, 2021 ). Ia juga gagal memprediksi perataanversus data overshoot yang diamati untuk bilangan Mach yang sangat besar pada Gambar 3 dan ditunjukkan dalam Madanian et al . Selain ukuran yang jauh lebih besar, ada dua faktor yang berbeda antara guncangan haluan antarplanet dan planet yang mungkin berkontribusi pada potensi guncangan silang rata-rata dan dinamis yang berbeda. Pertama, interaksi dinamis (perbincangan silang) antara sisi kuasi-paralel dan kuasi-tegak lurus merupakan masalah konstan untuk guncangan haluan (Mitchell et al., 2012 ) tetapi tidak untuk guncangan IP. Kedua, guncangan IP lebih umum mempertahankan populasi partikel yang dipercepat Fermi, yang biasanya tidak terjadi pada guncangan haluan planet. Namun, studi statistik ekstensif di mana potensi guncangan silang pada guncangan IP ditentukan secara langsung dari pengukuran in situ dan membandingkannya dengan yang ditentukan pada guncangan haluan Bumi diperlukan untuk memperkuat klaim ini dengan benar dan lebih jauh memahami transisi guncangan antarplanet.
Mengenai perubahan
dengan
Seperti yang terlihat pada Gambar 6 , Gedalin ( 1997 ) dan Dimmock et al. ( 2012 ) menunjukkan bukti teoritis dan observasional tentang penurunan potensi guncangan silang (dari hulu ke hilir) dengan peningkatan bilangan Mach. Hal ini dapat membantu menjelaskan pergeseran ke arah yang lebih rendah
-nilai yang diamati pada Gambar 6 untuk meningkatkan rentang bilangan Mach dan karenanya hasil Gambar 6 mungkin diharapkan. Namun, studi yang lebih rinci tentang profil spasial potensi guncangan silang dalam transisi guncangan diperlukan untuk memisahkan potensi hulu ke overshoot dibandingkan dengan hulu ke hilir. Studi sebelumnya menunjukkan bahwa menentukan potensi guncangan silang dari pengukuran in situ bukanlah tugas yang mudah dan metode yang berbeda sering kali memberikan hasil yang sangat berbeda (Schwartz et al., 2021 ). Dalam Dimmock et al. ( 2012 ) mereka menentukan potensi guncangan silang (hulu ke hilir) pada guncangan haluan Bumi menggunakan wahana antariksa Cluster dan hasil mereka sangat sesuai dengan hasil Gambar 6i . Namun, sebagian kecil dari persilangan guncangan kami menghasilkan hasil yang tidak fisikal
-nilai (perhatikan nilai negatif pada Gambar 6i ). Alasan untuk ini tidak jelas, tetapi ini bisa menunjukkan keterbatasan rumus dalam Persamaan 3 yang digunakan untuk menentukan
Faktor lain mungkin adalah penentuan beta plasma. Dari Persamaan 3 , dapat ditunjukkan bahwa
Oleh karena itu, perkiraan yang berlebihan
bisa mengakibatkan hal negatif
nilai. Banyak persimpangan dengan nilai negatif
-nilai adalah guncangan IP pada 1 AU di mana beta plasma elektron yang tepat tidak dapat ditentukan. Secara umum, dari tiga parameter yang digunakan untuk menentukan potensi guncangan silang melalui Persamaan 3 , beta plasma
adalah yang paling tidak pasti. Demikian pula, kompresi overshoot yang diremehkan
juga bisa mengakibatkan
yang menurut Gambar 2 bisa jadi merupakan kasus untuk banyak guncangan IP namun juga sebagian kecil penyeberangan MMS.
Memisahkan lintasan IP dan Bumi menjadi rendah
dan tinggi
plasma beta terbukti memiliki dampak kecil pada hasil. Membandingkan lintasan busur kejut Bumi pada Gambar 4d dan 4e beserta kecocokan terbaiknya pada Tabel 1 , menunjukkan bahwa kedua set koefisien tersebut sangat mirip. Koefisien kejut IP pada Tabel 1 sedikit lebih berbeda. Namun, karena jumlah lintasan yang lebih sedikit dan ketidakpastian dalam plasma beta elektron
penentuan persimpangan tersebut, hasilnya cenderung mengandung ketidakpastian yang besar. Menariknya, baik beta rendah
kasus pada Tabel 1 menghasilkan suku konstan
untuk guncangan IP dan
untuk Bumi. Oleh karena itu, mereka tampaknya paling baik dijelaskan oleh beta plasma yang lebih besar dari satu
Untuk guncangan haluan Bumi, hal ini mungkin disebabkan oleh kurangnya penyeberangan di bawah
.
Ketergantungan potensi overshoot dan cross-shock terhadap sudut kejut
telah ditunjukkan dalam penelitian sebelumnya menjadi minimal atau tidak ada (Dimmock et al., 2012 ; Sulaiman et al., 2016 ). Kami melakukan penelitian serupa (tidak ditampilkan), dan tidak ada ketergantungan yang jelas pada sudut kejut. Ketidaktergantungan yang diamati pada sudut kejut dapat disebabkan oleh ketergantungan bilangan Mach dan beta plasma yang jauh lebih kuat. Oleh karena itu, ketergantungan sudut kejut bisa jadi lemah, dan penyelidikan yang tepat terhadap hal ini akan memerlukan sejumlah besar persimpangan yang memiliki rentang serupaDanuntuk sudut kejut yang berbeda.
Data yang disajikan pada Gambar 3 dan 4 menunjukkan beberapa variabilitas dalam overshoot. Ketika membandingkan overshoot yang diamati dengan simulasi hibrida 2D kami, sebagian besar variabilitas overshoot kemungkinan berasal dari variasi sepanjang permukaan guncangan (Gambar 7c ). Namun, hasil simulasi tampaknya tidak sepenuhnya sesuai dengan pengamatan menggunakan bilangan Mach yang serupa danrezim, seperti yang diilustrasikan pada Gambar 7d . Simulasi hibrida 2D gagal menangkap nilai sebaran dan nilai rata-rata dibandingkan dengan data observasi. Ini mungkin karena simulasi memiliki fluktuasi frekuensi tinggi yang terbatas (di atas overshoot) dan tidak ada turbulensi hulu yang akan mengurangi variabilitas. Pekerjaan di masa mendatang akan memperluas ruang parameter dengan kampanye simulasi khusus untuk berbagai bilangan Mach.
Kami berspekulasi bahwa variabilitas overshoot sebagian besar disebabkan oleh nilai-nilai yang sedikit berbeda dari potensi guncangan silang yang dinormalkan di sepanjang front guncangan. Menurut ekspresi analitis dalam Persamaan 3 yang disimpulkan oleh Gedalin ( 2021 ), potensi guncangan silang yang dinormalkanmenentukan kemiringan asimtotik dari kompresi overshootsehubungan dengan bilangan Alfven MachOleh karena itu, guncangan yang memiliki sifat serupaDantapi, sedikit berbeda-parameter akan menghasilkan overshoot magnetik yang berbeda. Hal ini juga dapat menjelaskan peningkatan variabilitas overshoot untuk meningkatkan nomor Mach, lihat Gedalin ( 2021 ). Pengetahuan pasti tentang variasi spasial dan/atau temporal dalam potensi guncangan silang masih kurang dipahami (Schwartz et al., 2021 ), dan bentuk sederhana yang digunakan dalam Gedalin ( 2021 ) dari penurunan potensial berkelanjutan di seluruh guncangan mungkin bukan deskripsi yang paling akurat (Lefebvre et al., 2007 ; Schwartz et al., 2011 ). Selain itu, untuk guncangan dengan bilangan Mach dan overshoot yang besar, refleksi ion akhirnya menjadi jenuh (Madanian et al., 2024 ) dan guncangan mulai menghilangkan energi melalui mekanisme lain seperti riak permukaan guncangan (Johlander et al., 2018 ; Khotyaintsev et al., 2024 ) dan akhirnya reformasi guncangan (Gedalin et al., 2023 ; Sulaiman et al., 2015 ).
Mengoreksi bilangan Mach Kronian dengan faktor 0,78 menempatkan persilangan Kronian dalam kesesuaian yang baik dengan persilangan Bumi. Oleh karena itu, offset yang diamati antara persilangan Kronian dan Bumi (lihat Gambar 3 ) kemungkinan besar disebabkan oleh penentuan bilangan Mach Kronian yang tidak in-situ. Ini berarti bahwa tekanan dinamis angin surya sedang ditaksir terlalu tinggi ketika menggunakan model bow shock empiris dari Formisano ( 1979 ) dan Went et al. ( 2011 ) untuk Bumi dan Saturnus. Ini tampaknya menjadi kasus untuk model Went et al. ( 2011 ) yang digunakan untuk Saturnus (Jackman et al., 2019 ). Asal usul pasti dari perkiraan yang terlalu tinggi tersebut perlu diselidiki tetapi berada di luar cakupan makalah ini. Faktor 0,78 yang dinyatakan dalam makalah ini dapat digunakan untuk memberikan perkiraan yang lebih akurat dari bilangan Mach Alfvén ketika menggunakan metode bow-shock-model-fit yang diuraikan dalam Went et al. ( 2011 ) dan (Sulaiman et al., 2016 ). Akan tetapi, hasil kami semata-mata didasarkan pada offset yang ditemukan di Burkholder et al. ( 2025 ), yang mempertimbangkan guncangan haluan Bumi. Mungkin juga ada faktor-faktor lain yang tidak diketahui yang berkontribusi terhadap perbedaan akhir antara lintasan guncangan haluan Bumi dan Saturnus. Misalnya, beta plasma di Saturnus masih merupakan kuantitas yang tidak diketahui dan model guncangan haluan Kronian lainnya mungkin menghasilkan hasil yang berbeda.
5 Ringkasan
Kami menggunakan wahana antariksa SolO dan MMS untuk mempelajari overshoot magnetik pada 37 lintasan antarplanet dan 444 lintasan busur kejut Bumi. Hasilnya dibandingkan dengan 466 lintasan busur kejut Saturnus yang diperoleh dari penelitian sebelumnya oleh Sulaiman dkk. ( 2016 ) dan simulasi hibrida 2D. Temuan utama kami adalah:
- Setidaknya diperlukan 200 titik data terukur dalam overshoot guncangan agar dapat mengukur overshoot guncangan secara akurat.
- Persimpangan kejut Kronian memperlihatkan offset overshoot ke arah angka Mach yang lebih tinggi dibandingkan dengan persimpangan kejut haluan Bumi. Hal ini diduga berasal dari metode non-in situ untuk menentukan angka Mach. Ketika dikoreksi, overshoot Kronian sejajar dengan overshoot Bumi.
- Dengan menggunakan IP dan persimpangan kejut bumi, kita menemukan kompresi overshootRberhubungan dengan bilangan Mach Alfven menurut hubungan empirisR2=0.74MA2+7.6.
- Guncangan IP tampaknya dijelaskan oleh potensi guncangan silang yang dinormalisasi lebih rendah2Φ/miVu2dibandingkan dengan guncangan busur Bumi. Potensi guncangan silang yang diperkirakan pada guncangan busur Bumi cenderung lebih tinggi pada lintasan bilangan Mach yang lebih rendah.
- Variabilitas overshoot tidak dapat sepenuhnya dijelaskan dan direproduksi oleh simulasi hibrida 2D.
