Abstrak
Studi ini secara sistematis mengevaluasi kinerja skema lapisan batas planet (PBL) Mellor-Yamada-Nakanishi-Niino-Eddy-Diffusion-Mass-Flux dalam model Weather Research and Forecasting (WRF) dalam simulasi kecepatan angin dekat permukaan di berbagai topografi di Negara Bagian New York (NYS). Kecepatan angin yang disimulasikan dibandingkan dengan pengukuran in-situ dari 22 lokasi permukaan, dikelompokkan ke dalam enam kategori topografi: dataran benua (CT), tepi danau (LS), lembah sungai (RV), Long Island (LI), Block Island (BI), dan laut lepas pantai (OO). Evaluasi kuantitatif berdasarkan Relative Euclidean Distance menunjukkan bahwa kecepatan angin di lokasi OO adalah yang paling akurat direproduksi, diikuti oleh kecepatan di lokasi LI, sementara model tersebut berkinerja kurang akurat untuk kelompok topografi yang tersisa. Kecepatan angin di lokasi CT cenderung ditaksir terlalu tinggi sekitar 1 m/s, meskipun variabilitas diurnal (DV) mereka tertangkap dengan baik. Sebaliknya, model tersebut meremehkan DV angin di lokasi LS, RV, LI, dan BI, dengan bias terbesar terjadi di LI dan BI, yang mengakibatkan kecepatan angin siang hari yang diremehkan dan/atau kecepatan angin malam hari yang dilebih-lebihkan. Angin OO menunjukkan variasi diurnal minimal, yang ditangkap secara akurat oleh model WRF kami. Variasi diurnal angin permukaan terkait erat dengan perkembangan PBL. Di antara indikator perkembangan PBL, bias suhu potensial permukaan paling kuat berkorelasi dengan bias kecepatan angin. Model WRF kami menghadapi tantangan dalam menangkap perbedaan antara angin yang dipengaruhi oleh sirkulasi lokal dan yang berada di dataran kontinental, dan angin yang jauh lebih kuat di OO dibandingkan dengan BI. Penyebab potensial untuk bias ini dibahas, yang menawarkan jalur untuk meningkatkan simulasi angin permukaan di masa mendatang.
Poin-poin Utama
- Simulasi Penelitian dan Perkiraan Cuaca kami dengan skema lapisan batas planet Mellor-Yamada-Nakanishi-Niino-Eddy-Diffusion-Mass-Flux menunjukkan bias kecepatan angin yang beragam pada topografi yang bervariasi
- Angin lepas pantai-samudra direproduksi paling baik, sedangkan variabilitas angin diurnal yang dipengaruhi oleh sirkulasi lokal diremehkan.
- Hambatan orografis sub-grid dan topografi pulau kecil yang belum terselesaikan akan memberikan manfaat pada simulasi angin dataran dan angin pulau lepas pantai.
Ringkasan Bahasa Sederhana
Mengevaluasi simulasi kecepatan angin dekat permukaan secara akurat dalam model atmosfer skala meso sangat penting untuk berbagai aplikasi, seperti prakiraan polusi udara. Studi ini menilai kinerja model WRF dalam simulasi kecepatan angin dekat permukaan di 22 lokasi di berbagai medan di NYS. Hasilnya menunjukkan fitur bias yang khas dalam kecepatan angin yang disimulasikan, tergantung pada jenis medan. Model WRF kami bekerja paling akurat dalam simulasi angin lepas pantai-samudra, dengan kinerja terbaik kedua untuk angin pesisir dan hasil yang sebanding di lokasi lain. Kecepatan angin di dataran dan pulau lepas pantai sangat dilebih-lebihkan, kemungkinan karena kesalahan representasi hambatan orografis. Bias suhu potensial permukaan menunjukkan korelasi tertinggi dengan bias kecepatan angin. Angin yang dipengaruhi oleh sirkulasi lokal sebagian besar berbeda dari yang ada di dataran benua, dan angin OO lebih kuat daripada yang ada di pulau lepas pantai—namun model tersebut kesulitan untuk menangkap perbedaan ini. Dengan mengeksplorasi potensi penyebab bias ini, studi ini membuka jalan untuk meningkatkan simulasi angin permukaan di masa mendatang.
1 Pendahuluan
Angin dekat permukaan (pada ketinggian 10 m) memberikan pengaruh signifikan pada aktivitas harian manusia dan sistem iklim Bumi. Misalnya, angin dekat permukaan yang ekstrem (misalnya, dalam badai) menimbulkan ancaman besar bagi kehidupan manusia dan infrastruktur, yang menyebabkan kerusakan besar. Selain itu, angin dekat permukaan berfungsi sebagai faktor utama yang mendorong transfer energi dalam antarmuka laut-atmosfer. Akibatnya, memastikan keakuratan prakiraan angin dekat permukaan dalam model atmosfer sangat penting untuk menjaga kehidupan dan properti manusia, serta untuk memodelkan sistem iklim Bumi dan perubahan iklim secara efektif. Selain itu, angin dekat permukaan dalam model atmosfer merupakan masukan penting untuk komponen lainnya. Misalnya, parameterisasi laju emisi debu (Donner et al., 2011 ) dan laju tiupan salju (Déry & Yau, 1999 ; Li & Pomeroy, 1997 ; Yang et al., 2010 ) bergantung pada informasi kecepatan angin dekat permukaan. Hal ini menggarisbawahi pentingnya simulasi angin dekat permukaan yang akurat untuk simulasi khusus seperti badai debu dan fenomena tiupan salju. Selain itu, perkiraan akurat angin dekat permukaan sangat penting untuk meningkatkan efisiensi dan mengurangi biaya pembangkitan energi angin. Oleh karena itu, mengevaluasi simulasi angin dekat permukaan dalam model atmosfer sangat penting.
Simulasi akurat kecepatan angin di dekat permukaan merupakan tantangan, karena (a) angin di dekat permukaan terkait erat dengan sekumpulan besar mekanisme fisika kompleks seperti pemaksaan atmosfer skala besar, pemaksaan sirkulasi lokal (misalnya, angin laut-darat), pemaksaan medan (misalnya, hambatan permukaan), perpindahan momentum oleh turbulensi atmosfer (Hu, Klein, & Xue, 2013 ; Lorente-Plazas et al., 2016 ; Sun et al., 2020 ), dan (b) sebagian besar proses fisika ini berada dalam skala subgrid bahkan untuk model atmosfer skala meso, dan parameterisasinya masih memiliki kekurangan.
Penelitian sebelumnya menggambarkan bahwa dalam model skala meso, bias angin dekat permukaan terutama berasal dari empat aspek (a) data (misalnya, analisis ulang): digunakan untuk menghasilkan kondisi awal dan batas, (b) jarak grid kasar, (c) skema parameterisasi lapisan permukaan, dan (d) skema parameterisasi PBL (Jiménez & Dudhia, 2013 ; Jiménez et al., 2012 ; Solbakken et al., 2021 ). Bias yang disebabkan oleh data analisis ulang umumnya kurang parah dibandingkan dengan yang dari sumber lain (Lee et al., 2015 ; Ramon et al., 2019 ). Gómez-Navarro et al. ( 2015 ) menunjukkan peran penting jarak grid dalam simulasi angin dekat permukaan, menunjukkan bahwa perubahan resolusi model dari 6 hingga 2 km secara signifikan meningkatkan kinerja model. Namun, menggunakan jarak grid yang lebih halus tidak selalu menjamin peningkatan dalam simulasi angin dekat permukaan. Misalnya, Solbakken et al. ( 2021 ) menemukan bahwa bias angin di dekat permukaan tidak berkurang secara nyata ketika jarak grid berkurang dari 3 menjadi 1 km. Skema PBL dan lapisan permukaan sangat penting untuk simulasi perpindahan momentum oleh turbulensi atmosfer dan dampak gaya permukaan (Hu et al., 2013a , 2013b ; Jiménez et al., 2012 ). Meskipun ada kemajuan yang stabil dalam meningkatkan skema PBL dan skema lapisan permukaan, ketidakpastian masih ada (Solbakken et al., 2021 ).
Turbulensi atmosfer bertindak sebagai mekanisme signifikan untuk mengubah angin dekat permukaan dengan mengangkut momentum ke bawah dari lapisan atmosfer atas. Dalam model atmosfer skala meso, transportasi momentum oleh turbulensi secara umum dapat dikategorikan ke dalam dua kelas: transportasi lokal (Nakanishi & Niino, 2004 , 2006 , 2009 ) dan transportasi non-lokal (Hong et al., 2006 ; Pleim, 2007 ; Troen & Mahrt, 1986 ). Transportasi momentum lokal terutama terjadi melalui difusi turbulensi oleh pusaran skala kecil, yang pada dasarnya mendistribusikan kembali momentum atmosfer antara lapisan model yang berdekatan. Sebaliknya, transportasi momentum non-lokal mendistribusikan kembali momentum di beberapa lapisan model oleh pusaran turbulen besar yang terorganisir dengan baik. Parameterisasi transportasi sifat atmosfer (misalnya, momentum) oleh turbulensi skala kecil dan besar, biasanya dikembangkan berdasarkan simulasi pusaran besar jangka pendek (LES) daripada pengamatan. Namun, penting untuk dicatat bahwa LES mungkin tidak secara komprehensif menangkap keragaman dan kompleksitas skenario PBL, yang dapat menyebabkan ketidakpastian dalam perpindahan momentum (Ito et al., 2015 ; Nakanishi & Niino, 2009 ). Lebih jauh lagi, karena interaksi yang kompleks antara permukaan medan dan turbulensi, ketidakpastian apa pun dalam merepresentasikan mekanisme perpindahan ini dapat menyebar dan menyebabkan bias yang beragam dalam pemodelan angin dekat permukaan di berbagai jenis medan.
Bias dalam pemodelan angin dekat permukaan juga terkait erat dengan skema lapisan permukaan. Pertama, kecepatan angin dekat permukaan biasanya berkurang secara signifikan karena hambatan permukaan (yaitu, gesekan antara angin dekat permukaan dan permukaan medan). Mengukur hambatan permukaan ini biasanya memerlukan kecepatan gesekan (yaitu, u*), yang diperoleh dari skema lapisan permukaan. Skema PBL dalam model skala meso umumnya meparameterkan hambatan permukaan dengan memperkenalkan istilah sink dalam persamaan momentum untuk lapisan atmosfer terendah (misalnya, skema Yonsei University dan Mellor-Yamada-Nakanishi-Niino (MYNN) dalam model WRF, lihat kode sumbernya). Namun, parameterisasi hambatan permukaan sering mengabaikan pertimbangan eksplisit hambatan skala subgrid, yang mengakibatkan perkiraan berlebihan kecepatan angin dekat permukaan, karena hambatan permukaan subgrid dapat sebanding dalam besarnya dengan hambatan permukaan skala grid (Jiménez & Dudhia, 2012 ). Kedua, lapisan permukaan tunduk pada fluks pemanasan permukaan (misalnya, pemanasan laten dan sensibel) yang berpotensi menyebabkan suhu potensial yang lebih tinggi di lapisan permukaan dibandingkan dengan lapisan atas, sehingga meningkatkan ketidakstabilan atmosfer (Stull, 1988 ). Akibatnya, pengembangan PBL dan pencampuran turbulensi diintensifkan, sehingga mendorong transportasi momentum ke bawah dan meningkatkan kecepatan angin dekat permukaan. Ini menunjukkan bahwa ketidakpastian dalam fluks pemanasan permukaan, jika ada, merupakan penjelasan masuk akal lainnya untuk bias pemodelan dalam prediksi angin dekat permukaan. Mirip dengan parameterisasi PBL, bias angin dekat permukaan oleh kekurangan dalam skema lapisan permukaan sering menunjukkan fitur yang beragam di berbagai jenis medan.
Penelitian sebelumnya menunjukkan bahwa angin dekat permukaan yang disimulasikan oleh model skala meso memiliki bias yang jelas dan selanjutnya bias ini menunjukkan karakteristik yang berbeda di seluruh jenis orografis yang berbeda (Hu et al., 2010 , 2013a ; Zhang & Zheng, 2004 ). Misalnya, Jiménez dan Dudhia ( 2012 ) menunjukkan bahwa model WRF melebih-lebihkan kecepatan angin dekat permukaan di lembah dan dataran sebesar 1,06 m/s, tetapi meremehkan kecepatan angin dekat permukaan di pegunungan sebesar 2,93 m/s. Selain itu, menambahkan hambatan permukaan skala subgrid dapat secara dramatis mengurangi perkiraan yang terlalu rendah dari angin dekat permukaan di pegunungan dari 2,93 menjadi 0,22 m/s ketika atmosfer stabil (Lorente-Plazas et al., 2016 ). Zhang dan Zheng ( 2004 ) menunjukkan bahwa kecepatan angin dekat permukaan di dataran besar selatan biasanya diremehkan pada siang hari tetapi dilebih-lebihkan pada malam hari. Sebaliknya, angin lepas pantai pada siang hari dan malam hari ditaksir terlalu tinggi, yang disebabkan oleh ketidakmampuan parameterisasi turbulensi untuk mereproduksi perpindahan momentum dalam PBL (Shimada & Ohsawa, 2011 ). Jelas, evaluasi kecepatan angin yang ditujukan pada jenis medan tertentu (misalnya, wilayah pegunungan) mungkin tidak berlaku secara universal untuk medan lain (misalnya, wilayah pesisir). Akibatnya, melakukan perbandingan antara simulasi angin dekat permukaan di berbagai jenis medan dapat memberikan wawasan tentang kemampuan model untuk mereproduksi variasi kecepatan angin secara akurat di berbagai lanskap.
Tinjauan komprehensif dari literatur yang ada mengungkapkan perbedaan penting di antara model dalam kapasitas mereka untuk secara akurat mereplikasi kecepatan angin dekat permukaan di berbagai jenis medan. Meskipun demikian, evaluasi sistematis yang mencakup berbagai medan jarang dilakukan tetapi sangat penting (Lorente-Plazas et al., 2016 ; Shimada et al., 2011 ). Topografi Negara Bagian New York (NYS) mencakup spektrum medan termasuk dataran, gunung, lembah, wilayah pesisir, pulau, dan laut lepas pantai (OO). Ini memberikan peluang luar biasa untuk menilai kapasitas model WRF untuk menangkap angin dekat permukaan di bawah berbagai medan yang berbeda. Selain itu, aspirasi energi terbarukan yang diuraikan dalam Visi Baru NYS ( https://rev.ny.gov/ ) menetapkan peningkatan substansial dalam listrik dari sumber terbarukan, dengan energi angin memainkan peran yang signifikan. Akibatnya, studi ini bertujuan untuk mengidentifikasi bias pemodelan sistematis dalam kecepatan angin dekat permukaan di enam kategori medan utama yang berbeda dari topografi NYS. Investigasi ini akan menyelidiki penyebab bias pemodelan ini, sehingga memberikan wawasan untuk meningkatkan skema parameterisasi.
Sisa artikel ini disusun sebagai berikut. Bagian 2 menyajikan data observasi dan pengaturan simulasi. Bagian 3 mengkaji kinerja model dalam simulasi kecepatan angin di dekat permukaan. Bagian 4 membahas interpretasi fisik ketidakpastian dalam simulasi kecepatan angin di dekat permukaan. Kesimpulan utama kami dirangkum dalam Bagian 5 .
2 Pengaturan Percobaan
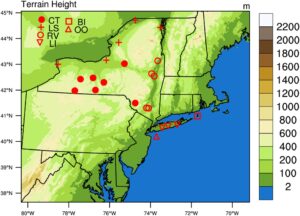
2.1 Data Observasi dan Klasifikasi Topografi
Kami menggunakan data kecepatan angin permukaan dekat observasional yang diukur di lokasi permukaan untuk mengevaluasi kinerja model. Periode waktu data ini mencakup dari 26 Februari 2018 hingga 28 Februari 2019. Lokasi observasional ini, yang berjumlah total 22 di seluruh NYS, dikategorikan ke dalam enam kelompok berbeda berdasarkan lokasi geografis dan karakteristik medannya: dataran kontinental (CT), Long Island (LI), lembah sungai (RV), tepi danau (LS), Block Island (BI), dan OO. Data yang dikumpulkan di lokasi ini mewakili angin permukaan dekat yang umum di atas dataran, pesisir Great Lakes, Hudson RV, wilayah pesisir, pulau kecil, dan OO di NYS. Data tersebut bersumber dari observasi permukaan per jam Amerika Serikat dan Kanada (USCSHO) dan Sistem Pengambilan Data Asimilasi Meteorologi (MADIS). Kecepatan angin permukaan dekat diukur menggunakan anemometer cangkir dan baling-baling yang diposisikan pada ketinggian 10 m, dengan ketidakpastian dalam ±1%. Informasi terperinci mengenai pengelompokan lokasi dan jenis medan dapat ditemukan pada Tabel S1 di Informasi Pendukung S1 dan Gambar 1 .
Untuk mengidentifikasi kemungkinan penyebab bias dalam simulasi angin dekat permukaan, kami mengeksplorasi korelasi antara bias angin dekat permukaan dan bias dalam keadaan atmosfer lain di permukaan, termasuk suhu, suhu potensial, rasio pencampuran uap, dan perubahan tekanan permukaan 3 jam yang diukur di lokasi permukaan. Pengukuran suhu diperoleh menggunakan termometer yang diposisikan pada ketinggian 1,25–2 m di atas permukaan tanah, dengan ketidakpastian kurang dari 0,1°C (Vincent et al., 2007 ). Rasio pencampuran uap air (
) diberikan sebagai
, Di mana
tekanan uap dihitung dengan persamaan Tetens dan suhu titik embun diukur,
diukur tekanannya, dan
sama dengan 0,622. Selain itu, data iradiasi surya ke bawah yang diambil dari Satelit Lingkungan Operasional Geostasioner (GOES) digunakan untuk menyelidiki korelasi antara bias iradiasi surya dan bias angin dekat permukaan. Ketidakpastian yang terkait dengan pengambilan iradiasi surya oleh GOES biasanya berkisar antara 2% hingga 5% (Habte et al., 2013 ). Data iradiasi surya diambil sampelnya dari sel grid GOES yang paling dekat dengan situs MADIS yang sesuai. Semua pengukuran adalah kuantitas sesaat dengan resolusi waktu 1 jam. Proses kontrol kualitas data mengecualikan kolom data apa pun yang berisi nilai yang hilang untuk setiap status atmosfer. Setelah itu, setiap situs pengukuran menghasilkan lebih dari 7.500 sampel (Tabel S1 dalam Informasi Pendukung S1 ).
2.2 Konfigurasi dan Simulasi Model WRF
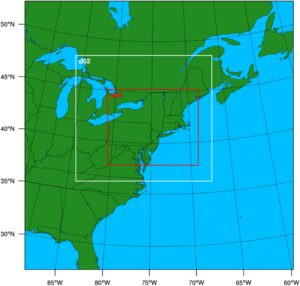
Kami menggunakan model Advanced Research WRF versi 4.1.2 (WRF-4.1.2) untuk melakukan simulasi angin dekat permukaan (Skamarock et al., 2019 ). Konfigurasi model kami menggunakan tiga domain bersarang dengan jarak grid masing-masing 36, 12, dan 3 km, dengan domain ketiga meliputi NYS (Tabel 1 dan Gambar 2 ). Domain model memiliki 35 lapisan sigma yang memanjang dari permukaan hingga 100 hPa, dengan 20 lapisan terletak di bawah 2 km. Kondisi awal dan batas berasal dari data analisis ulang global FNL dengan jarak grid 0,25° dan interval waktu 6 jam (Kalnay et al., 1996 ). Informasi indeks penggunaan lahan permukaan berasal dari versi modifikasi Noah dari data penggunaan lahan International Geosphere-Biosphere Program Moderate Resolution Imaging Spectroradiometer, dengan resolusi ∼900 m. Model ini diintegrasikan selama periode 1 tahun, mulai dari 26 Februari 2018 hingga 28 Februari 2019, untuk memastikan analisis statistik yang kuat di keempat musim. Simulasi dimulai ulang setiap 72 jam, dengan 12 jam awal ditetapkan sebagai waktu spin-up. Simulasi tumpang tindih untuk mencakup periode spin-up. Medan suhu dan uap air didorong dalam domain pertama dan kedua untuk mengurangi ketidakpastian dalam kondisi meteorologi ini (Gambar 2 ). Model menghasilkan keluaran pada interval per jam, yang terdiri dari kecepatan angin yang diukur pada ketinggian 10 m, suhu, suhu potensial, dan rasio pencampuran uap air pada ketinggian 2 m, dan iradiasi matahari permukaan dan tekanan permukaan di permukaan medan.
| Pengaturan model | |
|---|---|
| Durasi simulasi | 00:00 UTC 26/02/2018 18:00 UTC 28/02/2019 |
| Resolusi horizontal (km) | 36/12/3 (masing-masing untuk Domain1, Domain2, dan Domain3) |
| Titik grid (timur-barat, utara-selatan) | 80 × 80/121 × 112/321 × 269 (masing-masing untuk Domain1, Domain2, dan Domain3) |
| Tingkat vertikal | 35 |
| Kondisi awal | Sistem prakiraan global (GFS) final (FNL) Pusat Nasional untuk Prediksi Lingkungan (NCEP) |
| Skema fisik: | |
| Konveksi dangkal | MYNN-EDMF (Olson dkk., 2019 ) |
| Lapisan batas planet | MYNN-EDMF (Nakanishi & Niino, 2006 ) |
| Lapisan permukaan | Skema MM5 yang direvisi (Jiménez & Dudhia, 2012 ) |
| Permukaan tanah | Nuh (Niu dkk., 2011 ) |
| Konveksi dalam | Grell-3 (Grell, 1993 ; Grell & Dévényi, 2002 ) |
| Mikrofisika | Thompson (Thompson dkk., 2008 ) |
| Gelombang pendek | RRTMG (Iacono dkk., 2008 ) |
| Gelombang panjang | RRTMG (Iacono dkk., 2008 ) |
Model kami mengintegrasikan WRF-4.1.2 dengan skema parameterisasi MYNN PBL yang ditingkatkan (Mellor & Yamada, 1982 ; Nakanishi & Niino, 2009 ; Olson et al., 2019 ). Skema MYNN-Eddy-Diffusion-Mass-Flux (EDMF) menyatukan transportasi variabel keadaan atmosfer menggunakan difusi eddy (ED) dan fluks massa (MF), dengan demikian mengatasi masalah parameterisasi terpisah untuk transportasi lokal oleh turbulensi skala kecil dan transportasi non-lokal oleh turbulensi skala besar (Olson et al., 2019 ). Lebih jauh lagi, skema lapisan permukaan MM5 yang direvisi digunakan karena kinerjanya yang unggul dibandingkan dengan versi asli dalam mensimulasikan evolusi lapisan permukaan di bawah kondisi atmosfer yang stabil dan tidak stabil (Jiménez et al., 2012 ). Difusi turbulensi dalam PBL disimulasikan menggunakan skema penutupan orde MYNN 2,5, yang dikenal karena keunggulannya dalam mensimulasikan fluks laju pemanasan yang mengatur pengembangan PBL dan difusi momentum dibandingkan dengan skema penutupan orde lebih rendah (Sun et al., 2020 ).
Skema parameterisasi kunci lainnya mencakup skema mikrofisika awan yang peka aerosol Thompson-Eidhammer (Thompson & Eidhammer, 2016 ; Thompson et al., 2004 , 2008 ) untuk pemodelan proses mikrofisika awan, skema kumulus Grell-Freitas (Grell & Freitas, 2014 ) (diterapkan dalam domain satu dan dua) untuk mensimulasikan konveksi dalam, dan skema radiasi Rapid Radiative Transfer Model for General Circulation Models (RRTMG; Iacono et al., 2008 ) untuk radiasi gelombang pendek dan gelombang panjang. Rincian lebih lanjut mengenai skema parameterisasi ini disediakan dalam Tabel 1 .
2.3 Skema Parameterisasi Utama untuk Angin Dekat Permukaan
Untuk memudahkan analisis dan pemahaman fisik tentang bias pemodelan angin dekat permukaan, sub-bagian ini merinci skema lapisan permukaan dan skema PBL yang mengatur evolusi angin dekat permukaan dan persamaan utama dirangkum dalam Informasi Pendukung S1 .
2.3.1 Skema Lapisan Permukaan MM5 yang Direvisi
Skema lapisan permukaan MM5 yang direvisi digunakan untuk menghitung parameter utama seperti kecepatan gesekan (yaitu, u*), efisiensi pertukaran panas, dan efisiensi pertukaran kelembapan, yang memainkan peran penting dalam parameterisasi hambatan permukaan, fluks panas laten dan sensibel permukaan. Efisiensi u* dan pertukaran diturunkan berdasarkan teori kesamaan Monin-Obukhov yang merupakan fungsi kesamaan yang dikembangkan dengan baik yang sesuai untuk kondisi yang sangat stabil, netral, dan tidak stabil (Cheng & Brutsaert, 2005 ; Fairall et al., 1996 ). Selain itu, Jiménez et al. ( 2012 ) merevisi batas bawah u* dari 0,1 m/s menjadi 0,001 m/s, menghasilkan formulasi lapisan permukaan yang cocok untuk spektrum stabilitas atmosfer yang lebih luas. Selain itu, untuk permukaan air, skema MM5 yang direvisi menggabungkan perlakuan eksplisit kekasaran gelombang untuk mengkarakterisasi hambatan permukaan di atas badan air. Peningkatan ini menunjukkan keuntungan dalam simulasi angin dekat permukaan di atas lautan (Fairall et al., 2003 ).
2.3.2 Skema PBL MYNN-EDMF
Skema PBL MYNN-EDMF menghitung transpor turbulensi dari transpor keadaan atmosfer (misalnya, momentum) dengan menggabungkan komponen turbulensi skala kecil dan skala besar melalui integrasi mekanisme ED dan MF (Olson et al., 2019 ). Efisiensi transpor komponen ED ditentukan oleh tiga faktor utama: energi kinetik turbulensi (TKE), panjang pencampuran turbulensi, dan fungsi stabilitas. Dalam skema MYNN, TKE diramalkan oleh persamaan prognostik yang mempertimbangkan istilah sumber dan tenggelam TKE yang memperhitungkan difusi turbulensi, geser angin, efek daya apung, dan disipasi. Khususnya, representasi panjang pencampuran yang ditingkatkan telah diterapkan untuk meningkatkan interaksi dengan komponen MF, mencegah panjang pencampuran yang tidak wajar, dan mengurangi biaya komputasi. Fungsi stabilitas dalam skema diparameterisasi berdasarkan angka Richardson gradien dan dikalibrasi menggunakan konstanta penutupan yang dapat disetel yang berasal dari LES (Nakanishi & Niino, 2004 , 2006 , 2009 ). Sementara transpor ED selalu aktif, aktivasi transpor MF bersyarat pada pemenuhan tiga kriteria: (a) keberadaan gumpalan yang melebihi 100 m dalam ukuran total, (b) fluks daya apung positif, dan (c) lapisan super adiabatik yang memanjang 50 m di atas permukaan. Setelah pemenuhan kriteria ini, jumlah dan luas gumpalan turbulen skala sub-grid dihitung, dan integrasi vertikal berikutnya menggunakan model gumpalan massal yang menarik dilakukan untuk menghitung transpor keadaan atmosfer (misalnya, momentum).
3 Hasil
3.1 Evaluasi Kinerja Secara Keseluruhan
Bagian ini menilai kinerja keseluruhan model WRF kami dalam simulasi kecepatan angin dekat permukaan. Evaluasi sebelumnya terhadap simulasi angin dekat permukaan terutama berfokus pada bias kecepatan angin rata-rata (Jiménez & Dudhia, 2012 ), sering kali mengabaikan pertimbangan variabilitas kecepatan angin dan korelasi simulasi-observasi. Untuk mengukur secara komprehensif semua aspek kinerja model, studi ini menggunakan Jarak Euclidean Relatif (RED; Elmore & Richman, 2001 ; Wu et al., 2012 ). RED didefinisikan sebagai:

Di mana ”
” atau ”
” mewakili kecepatan angin permukaan dekat yang disimulasikan atau diamati pada N titik temporal (atau spasial) diskrit. RED terdiri dari tiga komponen: bias relatif kecepatan angin rata-rata (
), bias relatif variabilitas kecepatan angin (
), dan satu korelasi minus antara kecepatan angin yang diamati dan disimulasikan (
). Ketika digabungkan ke dalam rumus RED, ketiga komponen ini memberikan satu metrik tunggal yang merangkum kinerja model secara keseluruhan. Nilai RED yang lebih kecil dan komponen-komponennya menunjukkan kesesuaian yang lebih baik antara model dan pengamatan dalam aspek-aspek perilaku kecepatan angin yang sesuai. Secara khusus, AVG, STDDEV, dan OMCOR masing-masing menunjukkan kesalahan dalam rata-rata, variabilitas, dan korelasi. Oleh karena itu, RED mencerminkan kinerja model secara keseluruhan dengan mempertimbangkan ketiga aspek ini secara bersamaan. Sampai batas tertentu, RED mirip dengan Diagram Taylor karena komponen-komponennya memiliki interpretasi matematis yang serupa. RED bertujuan untuk memberikan penilaian yang komprehensif atas kinerja model dengan mempertimbangkan beberapa aspek statistik: rata-rata, variabilitas, dan bias korelasi, sedangkan Diagram Taylor mempertimbangkan kesalahan akar-rata-kuadrat (RMSE), deviasi standar, dan korelasi. Sementara RED adalah metrik numerik, Diagram Taylor adalah representasi grafis. Keduanya menawarkan ringkasan singkat kinerja model di berbagai ukuran statistik.
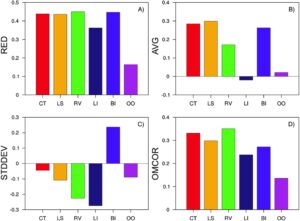
Kombinasi unik dari tiga komponen bias di situs OO menghasilkan RED terkecil sebesar 0,16, yang menunjukkan kinerja simulasi keseluruhan tertinggi dalam mereproduksi angin dekat permukaan (Gambar 3a ). Kinerja terbaik kedua adalah di situs LI, dengan RED sebesar 0,35. Sebaliknya, RED untuk kelompok situs lainnya (yaitu, CT, LS, RV, dan BI) sebanding satu sama lain dan sekitar 0,45, yang menunjukkan kinerja yang lebih buruk dibandingkan dengan situs OO dan LI. Analisis komponen bias mengungkapkan bahwa simulasi di situs LI dan OO menunjukkan besaran AVG terendah sekitar 0,02 (Gambar 3b ). Situs RV menampilkan kinerja terbaik kedua, dengan AVG sekitar 0,15, sedangkan AVG untuk situs lainnya serupa, berkisar sekitar 0,3. Khususnya, meskipun besarnya serupa, tanda AVG berbeda antara lokasi LI dan OO: negatif (menunjukkan kecepatan angin yang diremehkan) untuk LI dan positif (menunjukkan kecepatan angin yang dilebih-lebihkan) untuk OO. Selain itu, AVG yang rendah dapat disebabkan oleh bias kecil di semua kasus atau kompensasi antara bias positif dan negatif, yang menggarisbawahi perlunya penyelidikan lebih lanjut terhadap bias variabilitas kecepatan angin (yaitu, STDDEV). Dalam hal STDDEV, peringkat kinerja simulasi adalah CT, OO, LS, RV, BI, dan LI. Besarnya STDDEV untuk lokasi CT, OO, LS, dan RV meningkat dari -0,05 menjadi -0,23, yang menunjukkan perkiraan yang terlalu rendah dari variabilitas kecepatan angin pada berbagai tingkat di berbagai jenis topografi (Gambar 3c ). Sebaliknya, lokasi BI menunjukkan STDDEV sebesar 0,25, yang mewakili kinerja terburuk kedua dan disebabkan oleh perkiraan yang terlalu tinggi dari variabilitas kecepatan angin. STDDEV kelompok LI mendekati -0,3, dengan magnitudo terbesar di antara keenam kelompok, yang menunjukkan kinerja terburuk. Lebih jauh, meskipun simulasi kami menghasilkan AVG kecil di lokasi LI, simulasi ini secara signifikan meremehkan STDDEV, yang menunjukkan bahwa AVG kecil di lokasi LI (Gambar 3b ) mungkin disebabkan oleh kompensasi kesalahan. Simulasi kami menghasilkan koefisien korelasi kecepatan angin yang diamati-disimulasikan (OMCOR) terendah (yaitu, 0,14) untuk lokasi OO, OMCOR terendah kedua (yaitu, 0,24 dan 0,26) untuk lokasi LI dan BI, dan 0,29 hingga 0,35 untuk lokasi LS, CT, dan RV (Gambar 3d ).
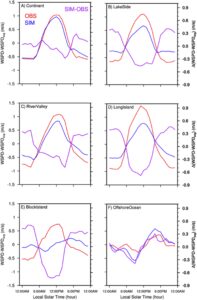
3.2 Variasi Harian Kecepatan Angin
Bagian ini menilai simulasi angin dekat permukaan kami dalam hal kecepatan angin DV. Kecepatan angin rata-rata yang diukur di lokasi permukaan daratan (yaitu, lokasi CT, LS, RV, LI, dan BI pada Gambar 4a–4e ) terutama berkisar dari 2 hingga 6 m/s dan menunjukkan siklus diurnal positif, dengan kecepatan angin siang hari jauh lebih tinggi daripada kecepatan angin malam (Yu et al., 2008 ). Perbedaannya bisa mencapai 2,5 m/s (Gambar 4d ). Sebaliknya, kecepatan angin di lokasi OO tidak menunjukkan variasi diurnal yang signifikan tetapi tetap kira-kira konstan pada 7 m/s (Gambar 4f ). Perbedaan ini dapat dikaitkan dengan fakta bahwa variasi diurnal suhu permukaan daratan biasanya 1,5 kali lebih besar daripada suhu permukaan laut (Kleidon & Renner, 2017 ), yang mengakibatkan perkembangan PBL diurnal yang jauh lebih kuat di daratan dibandingkan di atas lautan.
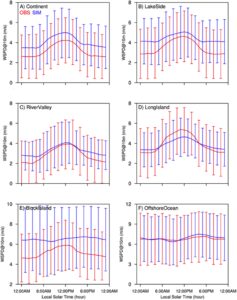
Kecepatan angin di lokasi CT menunjukkan estimasi berlebih yang konsisten sekitar 1 m/s, yang mencakup sekitar 30% dari nilai terukur dan tetap konsisten sepanjang hari (Gambar 4 dan Gambar S1a dalam Informasi Pendukung S1 ). Simulasi WRF kami melebih-lebihkan angin nokturnal di lokasi LS lebih dari 1 m/s, meskipun berkinerja lebih baik dalam simulasi angin siang hari (Gambar 4b dan Gambar S1b dalam Informasi Pendukung S1 ). Sebaliknya, estimasi berlebih angin RV pada malam hari kurang dari 1 m/s, tanpa bias signifikan dalam simulasi angin siang hari (Gambar 4c dan Gambar S1c dalam Informasi Pendukung S1 ). Bias angin di lokasi LI menunjukkan pola yang kontras: estimasi berlebih angin siang hari hingga 1 m/s, ditambah dengan estimasi berlebih angin nokturnal sebesar 0,5 m/s (Gambar 4d dan Gambar S1d dalam Informasi Pendukung S1 ). Simulasi WRF kami gagal menangkap variasi diurnal positif dari angin BI. Sementara pengukuran menunjukkan bahwa kecepatan angin siang hari di lokasi BI 1 m/s lebih tinggi daripada kecepatan angin tengah malam, dengan kecepatan rata-rata sekitar 5 m/s (Gambar 4e dan Gambar S1e dalam Informasi Pendukung S1 ), kecepatan angin yang disimulasikan menunjukkan variasi diurnal minimal, mempertahankan kecepatan yang kira-kira konstan sekitar 6,5 m/s sepanjang hari. Angin laut lepas pantai disimulasikan secara akurat oleh model kami dalam hal nilai rata-rata dan deviasi standar (Gambar 4f dan Gambar S1f dalam Informasi Pendukung S1 ).
Karakteristik AVG pada Gambar 3b sebagian dapat dijelaskan oleh bias dalam variasi diurnal kecepatan angin. Bias kecepatan angin kecil di situs OO sepanjang hari (Gambar 4f ) menunjukkan bahwa AVG rendah untuk situs OO pada Gambar 3b memang mencerminkan akurasi yang tinggi. Namun, AVG rendah untuk situs LI menyesatkan, karena muncul dari kompensasi antara perkiraan yang terlalu rendah selama siang hari dan perkiraan yang terlalu tinggi selama malam hari (Gambar 4d ). Sebaliknya, AVG untuk situs RV lebih besar daripada situs LI karena perkiraan yang terlalu tinggi yang lebih besar dari angin malam hari, sedangkan angin siang hari tidak mengalami perkiraan yang terlalu rendah (Gambar 4c ). AVG untuk situs CT, LS, dan BI adalah yang terbesar, terutama disebabkan oleh perkiraan yang terlalu tinggi secara sistematis, terutama terlihat selama malam hari (Gambar 4a, 4b , dan 4e ).
Untuk menganalisis bias variabilitas kecepatan angin, kami selanjutnya memeriksa DV angin dekat permukaan (Gambar 5 ), dan variabilitas harian (DTDV) (lihat definisi dalam Informasi Pendukung S1 ). DV di lokasi CT direproduksi dengan baik, dengan bias umumnya lebih kecil dari 0,2 m/s, kecuali pada pukul 4:00 sore dan 7:00 malam (Gambar 5a ), mungkin karena ketidakmampuan model kami untuk secara akurat menangkap pembentukan awan lapisan batas, evolusi selama sore hari, dan transisi selama malam hari (Shan et al., 2022 ). Selain itu, DTDV tidak menunjukkan bias yang jelas (lihat deviasi standar pada Gambar 4a ). Bias DV di lokasi OO menempati peringkat terendah kedua (Gambar 5f ), dan bias DTDV juga kecil (Gambar 4f ), yang menunjukkan bahwa model WRF kami bekerja relatif baik dalam mereproduksi variabilitas kecepatan angin di OO dibandingkan dengan kelompok lain. Sebaliknya, bias DV di lokasi LS, RV, dan LI positif selama malam hari dan negatif selama siang hari, dengan besaran mencapai hingga 0,4, 0,5, dan 0,6, masing-masing (Gambar 5b–5d ). Pola bias DV ini sesuai dengan STDDEV negatif pada Gambar 3c , yang menunjukkan perkiraan yang terlalu rendah dari kecepatan angin DV di lokasi ini. Bias DV di lokasi BI negatif (hingga -0,8 m/s; Gambar 5e ), sedangkan STDDEV untuk lokasi BI positif (Gambar 3c ). Perbedaan ini muncul karena DTDV untuk lokasi BI sangat diperkirakan terlalu tinggi (Gambar 4e ), yang mengalahkan perkiraan yang terlalu rendah dari DV.
3.3 Pengembangan PBL
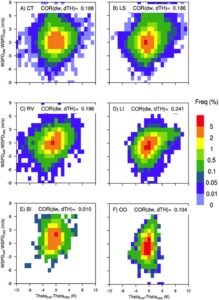
Variasi diurnal pada angin dekat permukaan terkait erat dengan pengembangan PBL. Hubungan ini menyiratkan bahwa bias dalam pengembangan PBL dapat menyebabkan pola angin dekat permukaan yang disimulasikan berbeda dari pengukuran, yang mengakibatkan bias korelasi (yaitu, OMCOR pada Gambar 3d ). Penggerak yang efektif sangat penting untuk memulai dan mempertahankan pengembangan PBL, sehingga menyebabkan variasi diurnal pada kecepatan angin dekat permukaan. Fluks pemanasan sensibel dan fluks pemanasan laten berfungsi sebagai penggerak termal yang signifikan untuk pengembangan PBL, sementara gangguan tekanan permukaan yang disebabkan oleh sistem cuaca sinoptik bertindak sebagai penggerak dinamis. Selain itu, iradiasi matahari ke bawah, yang memanaskan permukaan medan, berfungsi sebagai penggerak tidak langsung dari pengembangan PBL (Stensrud, 2007 ; Stull, 1988 ). Akibatnya, bias dalam penggerak PBL ini dalam simulasi WRF kami sebagian dapat menjelaskan bias korelasi dalam kecepatan angin (OMCOR) pada Gambar 3d . Dengan demikian, kami mengeksplorasi korelasi antara bias dalam penggerak PBL dan bias angin dekat permukaan. Dua penggerak PBL (yaitu, iradiasi horizontal global (GHI) dan gangguan tekanan 3 jam ( ∆p = 3 jam )) diukur secara langsung. Dalam skema lapisan permukaan MM5 yang direvisi, fluks pemanasan sensibel dan fluks pemanasan laten diparameterisasi berdasarkan suhu potensial ( θ = 2m ) dan rasio pencampuran uap air ( q = 2m ) di lapisan permukaan, yang menunjukkan bahwa bias dalam θ = 2m dan q = 2m dapat berfungsi sebagai indikator bias dalam fluks pemanasan sensibel dan fluks pemanasan laten, masing-masing (Jiménez et al., 2012 ).
Gambar 6 dan Gambar S2-S6 dalam Informasi Pendukung S1 mengilustrasikan korelasi antara bias dalam penggerak PBL atau indikatornya, dan bias angin dekat permukaan di semua kelompok lokasi. Secara umum, bias θ 2m menunjukkan korelasi yang lebih besar dengan bias angin dekat permukaan daripada bias penggerak atau indikator lainnya (yaitu, GHI, q 2m , dan ∆p 3hr ), yang menunjukkan bahwa bias dalam pengembangan PBL dan evolusi kecepatan angin dekat permukaan mungkin lebih erat kaitannya dengan pemanasan yang masuk akal di lapisan permukaan daripada penggerak lainnya. Mengingat bahwa penyelam pengembangan PBL primer, oleh karena itu kecepatan angin dekat permukaan, mungkin berbeda antara PBL yang tidak stabil (kebanyakan siang hari) dan yang stabil (kebanyakan malam hari), kami memeriksa korelasi antara bias θ 2m dan bias angin dekat permukaan untuk kondisi siang hari dan malam hari, secara terpisah (Gambar S5 dan S6 dalam Informasi Pendukung S1 ). Korelasi bias antara bias kecepatan angin dan bias θ 2m secara konsisten melebihi 0,25 selama siang hari dan malam hari di lokasi RV dan LI, yang patut diperhatikan. Estimasi berlebih dalam θ 2m menunjukkan estimasi berlebih dari fluks pemanasan yang masuk akal, yang mengakibatkan perkembangan PBL yang sangat kuat yang mentransfer momentum berlebihan dari PBL atas ke lapisan permukaan, yang menyebabkan estimasi berlebih dari kecepatan angin dekat permukaan. Sebaliknya, θ 2m yang diremehkan menyebabkan kecepatan angin dekat permukaan yang diremehkan melalui mekanisme yang sama tetapi dalam arah yang berlawanan.
Selain itu, T 2m berfungsi sebagai indikator untuk radiasi netto dan fluks pemanas di lapisan permukaan, yang memanaskan lapisan permukaan dan memulai pengembangan PBL (Stensrud, 2007 ). Gambar 7 mengilustrasikan variasi diurnal dalam bias kecepatan angin dekat permukaan dan bias suhu, mengungkapkan perkiraan yang lebih rendah dari t 2m sebesar 0–3 K pada siang hari, bertepatan dengan perkiraan yang lebih rendah dari kecepatan angin sebesar 0,5 hingga 1 m/dtk. Lebih jauh lagi, ketika t 2m ditaksir terlalu tinggi hingga 6 K, kecepatan angin dekat permukaan ditaksir terlalu tinggi hingga 1,5 m/dtk. Korelasi dalam bias t 2m dan bias kecepatan angin pada Gambar 7d ini lebih kuat daripada korelasi di lokasi lain, kemungkinan terkait dengan angin laut-darat, yang merupakan sirkulasi lokal paling kuat dibandingkan dengan angin sungai-lembah dan angin danau-darat. Pada siang hari, angin laut mengangkut udara dingin dari lautan ke daratan, yang menyebabkan lapisan-lapisan di daratan menjadi tidak stabil (Miller et al., 2003 ). Radiasi neto dan fluks pemanas yang diremehkan pada lapisan permukaan, ditunjukkan oleh perkiraan yang terlalu rendah t 2m , melemahkan perkembangan PBL relatif terhadap kondisi yang realistis, sehingga menghasilkan angin dekat permukaan yang diremehkan. Sebaliknya, ketika angin darat mendominasi pada malam hari, perkembangan PBL ditekan dalam kondisi yang stabil. Radiasi neto dan fluks pemanas yang diremehkan pada lapisan permukaan dapat menyebabkan percampuran turbulensi yang terlalu kuat, yang menyebabkan kecepatan angin dekat permukaan yang diremehkan (Crosman & Horel, 2010 ; Steele et al., 2013 ). Perlu juga dicatat bahwa korelasi yang jelas antara bias angin dekat permukaan dan t 2m ini tidak diamati di kelompok lokasi lain (Gambar 7 ), kemungkinan karena sirkulasi lokal yang lebih lemah atau tidak ada.

3.4 Keanekaragaman Angin di Dekat Permukaan
Dalam bagian ini, kami memperlakukan angin CT sebagai angin permukaan yang umum yang terutama dipengaruhi oleh daratan datar. Sebaliknya, angin permukaan di lokasi LS, RV, dan LI dipengaruhi oleh daratan datar dan sirkulasi atmosfer lokal (yaitu, angin danau, angin RV, dan angin laut). Sirkulasi lokal ini menyebabkan variasi yang signifikan dalam perkembangan PBL dan kondisi lapisan permukaan dibandingkan dengan daratan datar. Akibatnya, lokasi-lokasi ini menunjukkan pola angin permukaan yang berbeda dari yang ada di lokasi CT. Demikian pula, angin OO mewakili angin lepas pantai yang umum di atas permukaan laut terbuka, yang sebagian besar diatur oleh perkembangan PBL laut dan kondisi lapisan permukaan yang khusus untuk lingkungan laut terbuka. Sebaliknya, angin BI merujuk pada angin di pulau skala kecil, yang berbeda dari angin lepas pantai yang umum karena pengaruh pulau tersebut. Bagian ini bertujuan untuk mengevaluasi atribut unik angin LS, RV, LI, dan BI dibandingkan dengan pola angin umum (angin CT dan angin OO) untuk mengukur keakuratan simulasi WRF kami dalam mewakili keragaman angin dekat permukaan.
Pengukuran mengungkap variasi signifikan dalam kecepatan angin di antara kelompok situs yang berbeda, khususnya menyoroti bahwa angin LI dan LS lebih kuat daripada angin CT (Gambar 8a ). Perbedaan ini paling menonjol selama jam-jam dini hari (yaitu, 6:00 pagi hingga 9:00 pagi), dengan angin LI menunjukkan kecepatan hingga 1,2 m/s lebih tinggi dan angin LS hingga 0,5 m/s lebih tinggi daripada angin CT. Temuan ini menunjukkan bahwa pengaruh sirkulasi lokal seperti angin laut-darat dan angin danau-darat dapat menyebabkan angin dekat permukaan yang lebih kencang dibandingkan dengan kondisi daratan datar. Namun, simulasi model WRF kami menunjukkan perbedaan minimal dalam kecepatan angin antara situs LI dan CT (Gambar 8c ), sebagian besar disebabkan oleh perkiraan berlebihan angin CT (Gambar 4a ). Dalam kasus situs LS versus situs CT, perbedaan kecepatan angin yang disimulasikan lebih sesuai dengan pengukuran, meskipun model cenderung mencapai puncaknya pada sore hari, tidak seperti pengukuran (Gambar 8a dan 8c ). Pengukuran menunjukkan bahwa kecepatan angin RV cenderung lebih rendah daripada kecepatan angin CT, dengan perbedaan terbesar mencapai -0,5 m/s, yang kemungkinan dapat dikaitkan dengan efek sirkulasi sungai-lembah dan hambatan permukaan yang lebih kuat. Namun, kecepatan angin RV yang disimulasikan umumnya 1 m/s lebih rendah daripada kecepatan angin CT, yang mungkin dikaitkan dengan efek sirkulasi lokal yang terlalu tinggi atau hambatan permukaan yang terlalu rendah. Selain itu, angin CT yang terlalu tinggi juga berkontribusi terhadap perbedaan kecepatan angin yang terlalu rendah antara lokasi RV dan CT.
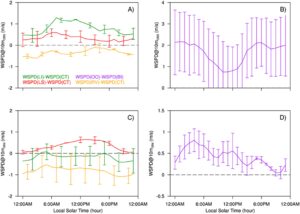
Pengukuran menunjukkan bahwa angin OO secara konsisten lebih kuat daripada angin BI, dengan perbedaan rata-rata berkisar antara 0,8 hingga 2,1 m/s (Gambar 8b ). Perbedaan ini terkait erat dengan dampak topografi pulau kecil, termasuk gaya termal dan dinamis. Kecepatan angin BI yang disimulasikan biasanya 0,2 hingga 0,7 m/s lebih tinggi daripada kecepatan angin OO, sebagian besar disebabkan oleh perkiraan angin BI yang terlalu tinggi (Gambar 4e dan 8d ). Hasil ini menunjukkan perkiraan yang terlalu rendah dari efek orografis BI dalam model.
4 Diskusi Lebih Lanjut
Analisis kami terhadap simulasi angin dekat permukaan di enam kategori topografi berbeda menunjukkan bahwa fitur bias bergantung secara signifikan pada konteks topografi spesifik. Seperti yang dicontohkan oleh situs CT yang dicirikan oleh tanah yang relatif datar, DV angin dekat permukaan direproduksi dengan baik (Gambar 5a ), tetapi kecepatan angin rata-rata ditaksir terlalu tinggi sebesar 1 m/s (Gambar 4a ). Sebaliknya, situs yang dipengaruhi oleh sirkulasi lokal (yaitu, situs LS, RV, dan LI) menunjukkan kecepatan angin DV yang diremehkan (Gambar 3b ). Perbedaan ini muncul dari perkiraan yang terlalu rendah terhadap kecepatan angin pada siang hari dan perkiraan yang terlalu tinggi pada malam hari (Gambar 5b–5d ). Bias dalam kecepatan angin rata-rata dan kecepatan angin DV kemungkinan terkait dengan parameterisasi hambatan permukaan serta parameterisasi transpor momentum (Berg et al., 2019 ; Jiménez & Dudhia, 2012 ; Yang et al., 2017 ). Bias korelasi harus dikaitkan dengan interaksi antara lapisan permukaan dan PBL. Pada bagian selanjutnya, kami berupaya untuk menetapkan hubungan antara bias angin dekat permukaan tertentu dan potensi kekurangan dalam skema PBL dan/atau lapisan permukaan.
4.1 Kekurangan Skema PBL
Perkembangan PBL menunjukkan variasi diurnal yang signifikan, yang mengakibatkan peningkatan transportasi momentum ke bawah, yang terutama disebabkan oleh difusi turbulensi lokal dan non-lokal pada siang hari, berbeda dengan kondisi malam hari. Mekanisme ini berkontribusi pada variasi diurnal positif yang diamati pada angin dekat permukaan. Akibatnya, masuk akal bahwa ketidakcukupan dalam parameterisasi difusi turbulensi lokal dan non-lokal dikaitkan dengan perkiraan yang terlalu rendah dari DV pada angin dekat permukaan. Dalam skema MYNN-EDMF, komponen ED dan MF berperan dalam parameterisasi transportasi momentum. Komponen ED, yang bertanggung jawab untuk mewakili ED skala kecil, beroperasi terus menerus sepanjang siang dan malam. Sebaliknya, komponen MF, yang memperhitungkan ED skala besar, diaktifkan secara kondisional, terutama pada siang hari. Kompleksitas dalam operasi skema ini berkontribusi pada beragam fitur bias angin dekat permukaan.
Seperti disebutkan dalam Bagian 2.3.2 , difusivitas momentum oleh komponen ED diatur oleh tiga faktor utama: TKE, panjang pencampuran turbulensi, dan fungsi stabilitas. Parameterisasi dari tiga faktor yang mengatur komponen ED mencakup penutupan yang ditentukan dan konstanta empiris lainnya. Konstanta ini mungkin tidak cocok secara universal untuk berbagai kondisi PBL. Misalnya, persamaan prognostik TKE berisi konstanta penutupan dalam istilah disipasi TKE (yaitu, B1 dalam Persamaan S1 dalam Informasi Pendukung S1 ; lihat juga Tabel S2 dalam Informasi Pendukung S1 ) dan B1 disetel terhadap hasil LES (Nakanishi & Niino, 2009 ). Penting untuk dicatat bahwa simulasi LES referensi yang dilakukan oleh Nakanishi dan Niino ( 2009 ) difokuskan secara khusus pada PBL konvektif selama jam-jam siang hari (yaitu, dari pukul 9:00 pagi hingga 4:00 sore) di wilayah dataran (Clarke et al., 1971 ). Nilai optimal untuk konstanta dalam skema MYNN, seperti konstanta penutupan (misalnya, B1) dan konstanta empiris lainnya (misalnya, α2 dalam Persamaan S12 di Informasi Pendukung S1 ), dapat bervariasi dengan rezim lapisan batas (Bodini et al., 2018 ; Lock & Mailhot, 2006 ). Ini menunjukkan bahwa konstanta yang disetel terhadap simulasi PBL siang hari di atas dataran mungkin tidak cocok untuk kondisi PBL nokturnal dan yang berada di wilayah pesisir yang dipengaruhi oleh sirkulasi lokal.
Komponen MF biasanya diaktifkan pada siang hari dan mendominasi transportasi momentum atas komponen ED (Olson et al., 2019 ). Kriteria ini sangat cocok untuk wilayah daratan datar, di mana faktor termal (misalnya, fluks pemanas dari permukaan medan) terutama mendorong konveksi lapisan batas dan konveksi dangkal di atasnya. Namun, kriteria ini mungkin menghadapi tantangan dalam secara akurat mewakili PBL konvektif yang dipicu oleh faktor dinamis, seperti pengangkatan orografis yang mendorong aliran udara ke atas (Mazon et al., 2015 ). Secara ilustratif, situs LI yang terletak di sepanjang pantai menunjukkan interaksi kompleks dari faktor dinamis dan termal dalam memicu PBL konvektif (Wai et al., 1996 ). Ini menyiratkan bahwa penghilangan faktor dinamis dalam pemicu komponen MF dapat mengakibatkan penghilangan turbulensi skala besar tertentu dalam PBL konvektif dan transportasi momentum terkaitnya, akibatnya mengarah pada perkiraan yang lebih rendah dari kecepatan angin dekat permukaan siang hari.
4.2 Kekurangan Skema Permukaan
Dalam simulasi WRF kami, bias angin di dekat permukaan juga dapat disebabkan oleh ketidakcukupan dalam representasi proses fisik lapisan permukaan. Misalnya, di lokasi CT, terdapat estimasi yang lebih tinggi dari kecepatan angin rata-rata sebesar 1 m/s sepanjang hari (Gambar 4a ). Bias yang berkelanjutan ini menunjukkan hubungan yang lebih mungkin dengan estimasi yang lebih rendah dari hambatan permukaan. Meskipun pilihan kami untuk jarak grid 3 km memungkinkan representasi hambatan permukaan skala grid sampai batas tertentu, tidak adanya penanganan eksplisit untuk hambatan permukaan skala sub-grid dapat berkontribusi pada estimasi yang lebih tinggi dari kecepatan angin di lokasi CT (Jiménez & Dudhia, 2012 ).
Tantangan dalam simulasi angin lepas pantai di lokasi BI kemungkinan muncul dari representasi properti permukaan. Sulit bagi sel grid 3 km kami untuk secara akurat mewakili medan BI, mengingat luasnya yang kecil hanya 25,2 km 2 (Gambar S7 dalam Informasi Pendukung). Keterbatasan ini menghasilkan perkiraan yang lebih rendah dari hambatan permukaan skala grid, yang mengarah ke perkiraan yang lebih tinggi secara signifikan dari kecepatan angin di BI, karena hambatan permukaan sangat penting untuk meredam angin dekat permukaan (Jiménez & Dudhia, 2012 ; Lorente-Plazas et al., 2016 ). Lebih jauh lagi, meskipun BI secara akurat direpresentasikan sebagai sel grid daratan dalam model, ukurannya yang kecil hanya mencakup tiga sel grid (Gambar S7 dalam Informasi Pendukung). Akibatnya, pengaruh daratan pada angin dekat permukaan minimal dan mudah ditimpa oleh efek laut karena adveksi, pencampuran, dan proses lainnya. Hal ini menyebabkan angin BI yang disimulasikan sangat dekat dengan angin OO (Gambar 4e dan 4f ). Sebaliknya, angin dekat permukaan di lokasi OO tereproduksi dengan baik, kemungkinan karena parameterisasi kekasaran gelombang yang lebih baik di wilayah laut terbuka dalam skema lapisan permukaan MM5 yang diperbarui (Fairall et al., 1996 , 2003 ).
4.3 Kekurangan pada Lapisan Permukaan dan Kopling PBL
Radiatif, masuk akal, dan fluks panas laten, mengganggu suhu permukaan (yaitu, t 2m ), adalah pemicu penting yang memulai pengembangan PBL konvektif. Bias dalam pemicu ini dapat menyebabkan PBL konvektif palsu atau hilang dan transportasi momentum yang didorong turbulensi terkait ke lapisan permukaan, sehingga menyebabkan korelasi dengan bias kecepatan angin dekat permukaan. Korelasi ini umumnya lebih kuat dalam kondisi atmosfer yang tidak stabil dibandingkan dengan kondisi stabil di mana PBL konvektif umumnya ditekan. Menggunakan situs LI sebagai contoh, dalam kondisi tidak stabil (yaitu, sebagian besar selama siang hari 7:00 pagi hingga 7:00 malam), bias t 2m positif dan negatif sering kali berhubungan dengan kecepatan angin dekat permukaan yang terlalu tinggi dan terlalu rendah, masing-masing (Gambar 7d ). Ini konsisten dengan korelasi tinggi (0,354) antara bias θ 2m dan bias kecepatan angin (Gambar S5d dalam Informasi Pendukung S1 ), karena fluks panas yang masuk akal bisa menjadi pemicu pengembangan PBL yang efisien dalam studi ini (Bagian 3.3 ). Dalam kondisi stabil (misalnya, sebagian besar selama malam hari pukul 7:00 malam hingga 7:00 pagi), estimasi angin yang berlebihan dengan bias t 2m positif tidak ada (Gambar 7d ), konsisten dengan korelasi bias kecepatan angin θ 2m yang lebih lemah (0,259, Gambar S6d dalam Informasi Pendukung S1 ). Perlu dicatat juga bahwa bias t 2m umumnya selaras dengan bias angin permukaan dalam tanda, tetapi tidak menunjukkan hubungan linear yang ketat (misalnya, Gambar 7c dan 7d ). Ini mungkin karena fluks radiatif dan pemanasan berfungsi sebagai pemicu awal untuk transportasi momentum, sementara difusivitas turbulensi dan hambatan permukaan terutama mengatur besarnya kecepatan angin permukaan.
Evolusi angin dekat permukaan terutama ditentukan oleh interaksi antara peningkatan melalui pengangkutan momentum dari lapisan atas dan disipasi karena hambatan permukaan. Keadaan ekuilibrium di mana faktor-faktor yang berlawanan ini mencapai keseimbangan bervariasi di seluruh lokasi medan, masing-masing dicirikan oleh efisiensi hambatan permukaan yang berbeda dan fitur sirkulasi lokal. Namun, menangkap variasi ini secara akurat dalam model kami merupakan tantangan. Misalnya, simulasi WRF kami menunjukkan bias dalam menangkap skenario bahwa angin LI lebih kuat daripada angin CT dan melebih-lebihkan perbedaan antara angin RV dan angin CT (Gambar 8a dan 8c ). Tantangannya mungkin terletak pada penerapan parameter konstan dalam aktivasi komponen MF, seperti lapisan super-adiabatik 50 m yang tetap. Konstanta empiris ini terbukti tidak memadai untuk penerapan universal di berbagai lokasi, di mana stabilitas atmosfer dipengaruhi oleh fitur medan yang berbeda dan sirkulasi lokal. Akibatnya, hal ini mengarah pada penghilangan atau kesalahan penyajian keragaman dalam kopling antara PBL dan permukaan medan. Akibatnya, simulasi WRF kami menemui kesulitan dalam menangkap secara akurat perbedaan sistematis antara angin di lokasi RV, LS, dan LI dibandingkan dengan angin di lokasi CT.
5. Penutup
Studi ini mengevaluasi kemampuan model WRF untuk secara akurat mensimulasikan kecepatan angin dekat permukaan di enam tipe topografi: dataran benua, tepi danau, lembah sungai, wilayah pesisir, pulau lepas pantai, dan lautan lepas pantai di NYS. Penilaian ini dilakukan dengan membandingkan simulasi 1 tahun dengan pengukuran in-situ untuk memeriksa kinerja model dalam menangkap pola angin dekat permukaan di berbagai medan. Selain itu, analisis difokuskan pada kekurangan dalam skema PBL dan skema lapisan permukaan, mengidentifikasi kontribusinya terhadap bias dalam simulasi kecepatan angin dekat permukaan. Temuan utama dirangkum di bawah ini.
Dengan menggunakan Relative Error Deviation dan komponen-komponennya untuk evaluasi yang komprehensif, simulasi WRF berkinerja terbaik dalam mereproduksi angin OO, dengan angin pesisir berada di peringkat kedua. Sebaliknya, kinerja di lokasi lain relatif lebih buruk. Simulasi untuk angin pesisir dan OO mengungguli yang lain dalam mereproduksi kecepatan angin rata-rata secara akurat. Simulasi angin RV menunjukkan kinerja terbaik kedua, sementara simulasi untuk lokasi lain sebanding. Dalam hal variabilitas kecepatan angin, simulasi untuk angin biasa dan OO berkinerja terbaik, dengan bias meningkat dalam urutan berikut: tepi danau, RV, pulau lepas pantai, dan pantai. Simulasi menunjukkan bias terendah dalam korelasi antara simulasi dan pengukuran untuk angin OO, dengan kinerja yang sebanding untuk lokasi lain.
Model WRF secara akurat menangkap variasi diurnal angin dekat permukaan di dataran khas yang bebas dari pengaruh sirkulasi lokal tetapi secara konsisten melebih-lebihkan kecepatan angin dataran sekitar 1 m/s. Variasi diurnal angin dekat permukaan di tepi danau, RV, dan lokasi pesisir lebih kuat daripada yang ada di lokasi dataran, kemungkinan dipengaruhi oleh sirkulasi lokal yang meningkatkan pengembangan PBL (Hsieh et al., 2022 ; Miller et al., 2003 ). Namun, simulasi WRF meremehkan variasi diurnal kecepatan angin dekat permukaan di lokasi ini, dengan kecepatan angin nokturnal yang terlalu tinggi di tepi danau dan lokasi pesisir, dan kecepatan angin siang hari diremehkan di lokasi pesisir (Gambar 4b–4d ). Simulasi WRF berhasil mereproduksi angin lepas pantai yang khas dan secara akurat menangkap kecepatan rata-rata, variabilitas, dan korelasi simulasi-pengukuran. Namun, pengaruh topografi BI menyebabkan variasi diurnal positif dalam angin pulau lepas pantai. Simulasi WRF, dengan jarak grid 3 km, kesulitan untuk mengatasi topografi BI, sehingga menyebabkan perkiraan kecepatan angin yang terlalu tinggi sebesar 2 m/s dan tidak memperhitungkan siklus diurnal angin pulau lepas pantai.
Dalam simulasi kami dengan jarak grid 3 km yang dioptimalkan untuk proses skala grid yang mengatur angin dekat permukaan (Gómez-Navarro et al., 2015 ; Solbakken et al., 2021 ), bias utama dalam angin dekat permukaan dikaitkan dengan kekurangan dalam skema PBL dan lapisan permukaan. Jarak grid 3 km diharapkan dapat secara efektif menangkap fitur medan skala grid di atas dataran. Akibatnya, perkiraan yang terlalu tinggi dari kecepatan angin dekat permukaan dataran kemungkinan besar disebabkan oleh kesalahan penyajian hambatan permukaan sub-grid. Kekurangan ini mungkin berasal dari skema MYNN-EDMF saat ini, yang tidak memiliki parameterisasi terkait. Investigasi di masa mendatang harus menggabungkan penanganan eksplisit untuk hambatan permukaan skala sub-grid (Jiménez & Dudhia, 2012 ) untuk meningkatkan akurasi simulasi angin dekat permukaan dataran.
Pemaksaan orografis pada pulau berskala kecil, seperti BI, menghasilkan variasi angin diurnal yang jelas, yang kontras dengan angin OO yang umum. Karena hambatan permukaan, kecepatan angin di lokasi pulau lepas pantai jauh lebih rendah daripada di lokasi OO. Akan tetapi, simulasi kami gagal menangkap variasi diurnal pada angin BI dan secara sistematis melebih-lebihkan kecepatan angin rata-rata sekitar 2 m/s. Perbedaan ini mungkin disebabkan oleh keterbatasan jarak grid 3 km, yang sulit untuk merepresentasikan topografi BI secara memadai, yang menyebabkan perkiraan yang lebih rendah dari hambatan permukaan skala grid.
Selain itu, perkembangan diurnal PBL di lokasi yang terdampak oleh sirkulasi lokal lebih kuat daripada di lokasi dataran. Akibatnya, DV angin dekat permukaan di tepi danau, RV, dan lokasi pesisir lebih kuat daripada di lokasi dataran. Simulasi WRF kami secara signifikan meremehkan DV angin di tepi danau, RV, dan lokasi pesisir, yang menunjukkan bahwa skema MYNN-EDMF gagal menangkap pengaruh sirkulasi lokal. Integrasi komponen ED dan MF merupakan kemajuan penting dalam menangani redistribusi momentum oleh turbulensi atmosfer skala besar dan kecil. Namun demikian, parameter yang dapat disetel konstan, seperti konstanta penutupan turbulensi dalam komponen ED dan ketebalan lapisan super-adiabatik yang ditentukan dalam kriteria aktivasi komponen MF, mungkin tidak menunjukkan penerapan universal di berbagai kondisi PBL (Nakanishi & Niino, 2009 ; Neggers, 2015 ; Neggers et al., 2009 ). Sangat penting untuk menilai dan menyesuaikan parameter ini berdasarkan pengukuran jangka panjang, bukan simulasi yang dibatasi kurang dari satu hari dan jenis lahan tertentu, seperti yang sering dilakukan di LES.
Interaksi antara lapisan permukaan dan turbulensi atmosfer biasanya mengatur pengembangan PBL dan, akibatnya, angin dekat permukaan. Fluks energi dari permukaan sering kali mendorong pengembangan PBL. Oleh karena itu, ketidakakuratan dalam simulasi pendorong ini dapat mengakibatkan bias dalam korelasi antara pengamatan dan pengukuran. Studi ini mengungkapkan bahwa bias suhu potensial permukaan menunjukkan korelasi terkuat dengan bias angin dekat permukaan, terutama di lokasi pesisir. Temuan ini menunjukkan bahwa fluks pemanasan yang masuk akal dari tanah dapat menjadi sumber bias yang cukup besar dalam pengembangan PBL, akibatnya memengaruhi korelasi antara kecepatan angin dekat permukaan yang diamati dan diukur.
Sangat penting untuk mengakui tantangan dalam mengisolasi kekurangan tertentu dalam skema PBL dan lapisan permukaan sebagai kontributor potensial terhadap bias angin dekat permukaan. Kompleksitas ini berasal dari interaksi rumit dalam lapisan permukaan dan PBL. Untuk mendapatkan wawasan yang lebih mendalam tentang penyebab fisik yang mendasari kekurangan model, penyelidikan di masa mendatang akan difokuskan pada evaluasi profil angin dan pemeriksaan sensitivitas parameter utama. Hasil dari penelitian ini akan dilaporkan dalam pekerjaan mendatang.
